Methods for estimating spectral reflectance from XYZ colorimetry were evaluated using a range of different types of training datasets. The results show that when a measurement dataset with similar primary colorants (and therefore having similar reflectance curves) are used for training, the RMSE errors and metameric differences under different illuminants are the lowest. This study demonstrates that, a training data can be mapped to represent spectral data for a group of print data based on matching material components (spectral similarity) with the test data, and obtain spectral estimates with satisfactory spectral and colorimetric outcomes. The findings suggest that using polynomial bases or colorimetric weighted bases with least squares fit produced estimated reflectances with low metameric mismatches under different illuminants. For the two best performing spectral estimation methods their ability to predict tristimulus values were assessed with tristimulus calculated using the measured reflectances and a destination illuminant. Their performances were also compared to the colour predictions obtained from different CATs and MATs under varying lighting conditions. The results show that a spectral estimation method with specific training dataset can serve as a good alternative to predict
Tanzima Habib, Phil Green, Peter Nussbaum, "Spectral Estimation: Its Behaviour as a SAT and Implementation in Colour Management" in Journal of Imaging Science and Technology, 2023, pp 1 - 23, https://doi.org/10.2352/J.ImagingSci.Technol.2023.67.6.060408
- received August 2023
- accepted December 2023
- PublishedNovember 2023
| Sl. No. | Polynomial Order | Terms |
|---|---|---|
| 1. | Second | 1, X, Y, Z, XY, XZ, Y Z, X2, Y 2, Z2 |
| 2. | Third | 1, X, Y, Z, XY, XZ, Y Z, X2, Y 2, Z2, XY 2, XZ2, X2Y, X2Z, Y 2Z, Y Z2, XY Z, X3, Y 3, Z3 |
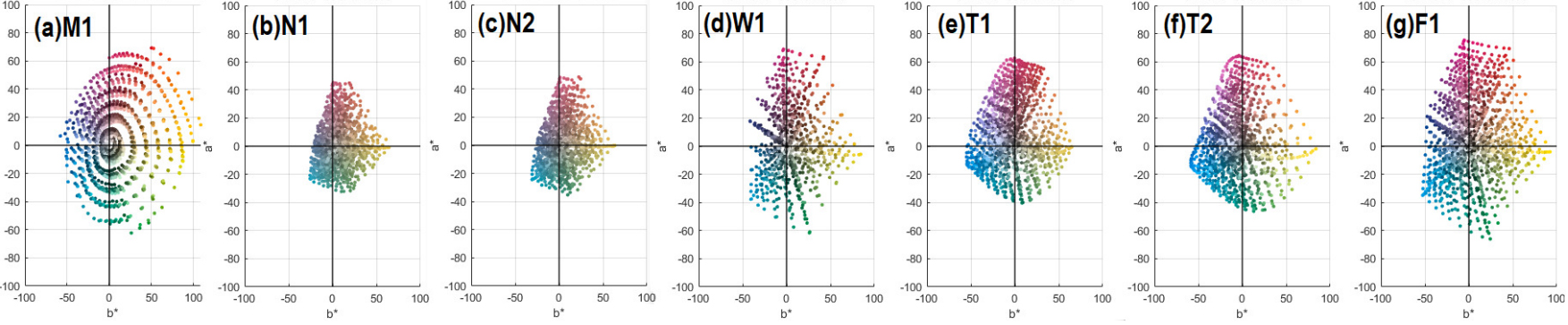
| Dataset | Substrate (L*, a*, b*) | No. of samples | Spectral range | Use in Test 1 | Use in Test 2 |
|---|---|---|---|---|---|
| Munsell glossy colour chip (M1) | — | 1600 | 380 nm–780 nm interval 5 nm | Training & test | Training |
| Offset litho on premium coated (F1) | (95, 1.5, − 6) | 1617 | 380 nm–730 nm interval 10 nm | Training & test | Training |
| Web offset on lightweight coated (W1) | (88.8, − 0.18, 3.7) | 1600 | 400 nm–700 nm interval 10 nm | Training & test | Training |
| Cold-set offset on newsprint (N1) | (81.9, − 0.79, 5.08) | 1485 | 380 nm–730 nm interval 10 nm | Training & test | Training & test |
| Cold-set offset on newsprint (N2) | (82.9, 0.31, 4.45) | 1485 | 380 nm–730 nm interval 10 nm | Training & test | Training & test |
| Digital print on textile (T1) | (87, 4.55, − 19.33) | 1485 | 380 nm–780 nm interval 10 nm | Training & test | Training & test |
| Digital print on textile (T2) | (94.52, 2.26, − 14.7) | 1485 | 380 nm–780 nm interval 10 nm | Training & test | Training & test |
| Identifier | Test data | Training data | Printing conditions | Substrates (Test/Training) |
|---|---|---|---|---|
| N2–M1 | N2 | M1 | Dissimilar | Newsprint/Colour chip |
| N2–W1 | N2 | W1 | Dissimilar | Newsprint/Light coated paper |
| N2–N1 | N2 | T1 | Similar | Newsprint/Newsprint |
| N1–N2 | N1 | N2 | Similar | Newsprint/Newsprint |
| T2–M1 | T2 | M1 | Dissimilar | Textile/Colour chip |
| T2–F1 | T2 | F1 | Dissimilar | Textile/Premium coated paper |
| T2–W1 | T2 | W1 | Dissimilar | Textile/Light coated paper |
| T2–T1 | T2 | N1 | Similar | Textile/Textile |
| T1–T2 | T1 | T2 | Similar | Textile/Textile |
| Dataset | Wiener | PCA | wPCA | PInverse | wPInverse | Polynomial 2 | Polynomial 3 | Waypoint-R |
|---|---|---|---|---|---|---|---|---|
| M1–M1 | 0.0410 | 0.0395 | 0.0278 | 0.0381 | 0.0236 | 0.0286 | 0.0249 | 0.0405 |
| F1–F1 | 0.0337 | 0.0212 | 0.0095 | 0.0246 | 0.0091 | 0.0094 | 0.0072 | 0.0364 |
| W1–W1 | 0.0241 | 0.0158 | 0.0073 | 0.0183 | 0.0063 | 0.0076 | 0.0062 | 0.0440 |
| N1–N1 | 0.0220 | 0.0120 | 0.0058 | 0.0135 | 0.0056 | 0.0055 | 0.0047 | 0.0397 |
| N2–N2 | 0.0216 | 0.0124 | 0.0059 | 0.0139 | 0.0060 | 0.0056 | 0.0046 | 0.0572 |
| T1–T1 | 0.0330 | 0.0254 | 0.0118 | 0.0275 | 0.0126 | 0.0140 | 0.0105 | 0.0476 |
| T2–T2 | 0.0394 | 0.0298 | 0.0139 | 0.0319 | 0.0132 | 0.0158 | 0.0119 | 0.0420 |
| Dataset | Wiener | PCA | wPCA | PInverse | wPInverse | Polynomial 2 | Polynomial 3 | Waypoint-R |
|---|---|---|---|---|---|---|---|---|
| M1–M1 | 0.3098 | 0.2944 | 1.1696 | 0.3080 | 0.3060 | 0.2919 | 0.2922 | 0.3057 |
| F1–F1 | 0.1012 | 0.0752 | 0.0469 | 0.0957 | 0.0310 | 0.0377 | 0.0348 | 0.1646 |
| W1–W1 | 0.0883 | 0.0720 | 0.0436 | 0.0838 | 0.0313 | 0.0288 | 0.0263 | 0.2485 |
| N1–N1 | 0.0662 | 0.0448 | 0.0267 | 0.0529 | 0.0180 | 0.0218 | 0.0207 | 0.1085 |
| N2–N2 | 0.0689 | 0.0515 | 0.0267 | 0.0587 | 0.0200 | 0.0232 | 0.0224 | 0.1440 |
| T1–T1 | 0.1172 | 0.0944 | 0.0427 | 0.1064 | 0.0345 | 0.0521 | 0.0297 | 0.1962 |
| T2–T2 | 0.1767 | 0.1345 | 0.0528 | 0.1608 | 0.0571 | 0.0735 | 0.0390 | 0.2233 |
| Dataset | Wiener | PCA | wPCA | PInverse | wPInverse | Polynomial 2 | Polynomial 3 | Waypoint-R |
|---|---|---|---|---|---|---|---|---|
| M1–M1 | 0.9778 | 0.9828 | 0.9724 | 0.9815 | 0.9896 | 0.9863 | 0.9885 | 0.9861 |
| W1–W1 | 0.9842 | 0.9831 | 0.9984 | 0.9893 | 0.9976 | 0.9955 | 0.9983 | 0.9913 |
| F1–F1 | 0.9870 | 0.9887 | 0.9986 | 0.9918 | 0.9984 | 0.9975 | 0.9986 | 0.9892 |
| N2–N1 | 0.9962 | 0.9985 | 0.9997 | 0.9985 | 0.9997 | 0.9997 | 0.9998 | 0.9904 |
| N1–N2 | 0.9960 | 0.9984 | 0.9997 | 0.9983 | 0.9996 | 0.9997 | 0.9998 | 0.9881 |
| T1–T1 | 0.9826 | 0.9909 | 0.9985 | 0.9868 | 0.9940 | 0.9970 | 0.9983 | 0.9850 |
| T2–T2 | 0.9805 | 0.9900 | 0.9968 | 0.9882 | 0.9972 | 0.9969 | 0.9982 | 0.9887 |
| Dataset | Wiener | PCA | wPCA | PInverse | wPInverse | Polynomial 2 | Polynomial 3 | Waypoint-R |
|---|---|---|---|---|---|---|---|---|
| M1–M1 | 0.59 (4.46) | 0.65 (4.02) | 0.3 (3.04) | 0.6 (4.33) | 0.32 (2.83) | 0.44 (3.04) | 0.32 (2.38) | 0.33 (2.52) |
| F1–F1 | 0.99 (3.99) | 0.84 (5.53) | 0.28 (1.5) | 0.71 (3.87) | 0.29 (1.27) | 0.34 (2.02) | 0.23 (0.96) | 0.48 (1.76) |
| W1–W1 | 0.82 (3.44) | 0.69 (4.38) | 0.27 (1.51) | 0.62 (3.26) | 0.25 (1.28) | 0.31 (1.78) | 0.24 (1.07) | 0.96 (3.92) |
| N1–N1 | 0.41 (1.42) | 0.28 (1.04) | 0.13 (0.6) | 0.27 (1.17) | 0.12 (0.43) | 0.12 (0.48) | 0.1 (0.46) | 0.66 (1.18) |
| N2–N2 | 0.38 (1.49) | 0.3 (1.16) | 0.13 (0.6) | 0.29 (1.3) | 0.13 (0.5) | 0.13 (0.51) | 0.1 (0.51) | 0.83 (1.86) |
| T1–T1 | 0.66 (3.07) | 0.66 (2.59) | 0.25 (1.27) | 0.6 (2.91) | 0.25 (1.35) | 0.35 (1.4) | 0.23 (1.04) | 0.61 (2.08) |
| T2–T2 | 0.79 (3.42) | 0.85 (2.78) | 0.34 (1.35) | 0.71 (3.15) | 0.32 (1.1) | 0.42 (1.69) | 0.31 (0.95) | 0.63 (1.95) |
| Dataset | Wiener | PCA | wPCA | PInverse | wPInverse | Polynomial 2 | Polynomial 3 | Waypoint-R |
|---|---|---|---|---|---|---|---|---|
| M1–M1 | 1.50 (12.31) | 1.67 (12.09) | 0.83 (13.8) | 1.52 (12.08) | 0.81 (8.26) | 1.13 (9.47) | 0.81 (7.07) | 0.83 (6.78) |
| F1–F1 | 0.99 (15.04) | 2.40 (14.39) | 0.82 (5.61) | 2.10 (14.43) | 0.83 (4.41) | 0.95 (5.68) | 0.66 (2.68) | 1.40 (6.71) |
| W1–W1 | 0.82 (11.95) | 1.97 (12.08) | 0.76 (5.46) | 1.79 (11.33) | 0.68 (3.38) | 0.85 (4.98) | 0.67 (3) | 2.74 (11.05) |
| N1–N1 | 0.41 (4.86) | 0.83 (3.5) | 0.38 (1.86) | 0.81 (4.01) | 0.36 (1.34) | 0.36 (1.43) | 0.31 (1.41) | 1.63 (3.52) |
| N2–N2 | 0.38 (5.33) | 0.88 (4.01) | 0.39 (1.84) | 0.84 (4.6) | 0.37 (1.52) | 0.37 (1.56) | 0.30 (1.55) | 2.20 (5.29) |
| T1–T1 | 0.66 (9.95) | 1.71 (8.02) | 0.62 (3.64) | 1.56 (9.29) | 0.57 (4.07) | 0.84 (3.46) | 0.54 (2.2) | 1.24 (6.49) |
| T2–T2 | 0.79 (11.03) | 2.21 (8.75) | 0.82 (4.15) | 1.84 (10.02) | 0.74 (3.4) | 1.00 (3.97) | 0.71 (2.03) | 1.35 (5.5) |
| Dataset | Wiener | PCA | wPCA | PInverse | wPInverse | Polynomial 2 | Polynomial 3 | Waypoint-R |
|---|---|---|---|---|---|---|---|---|
| N2–M1 | 0.0585 | 0.0489 | 0.0557 | 0.0516 | 0.0542 | 0.0586 | 0.0595 | 0.0573 |
| N2–W1 | 0.0331 | 0.0198 | 0.0186 | 0.0199 | 0.0175 | 0.0174 | 0.0176 | 0.0513 |
| N2–N1 | 0.0303 | 0.0178 | 0.0140 | 0.0190 | 0.0135 | 0.0137 | 0.0132 | 0.0572 |
| N1–N2 | 0.0231 | 0.0180 | 0.0139 | 0.0187 | 0.0140 | 0.0136 | 0.0132 | 0.0482 |
| T2–M1 | 0.0587 | 0.0571 | 0.0617 | 0.0564 | 0.0539 | 0.0587 | 0.0611 | 0.0646 |
| T2–F1 | 0.0417 | 0.0411 | 0.0349 | 0.0375 | 0.0311 | 0.0320 | 0.0313 | 0.0478 |
| T2–W1 | 0.0416 | 0.0427 | 0.0385 | 0.0405 | 0.0357 | 0.0346 | 0.0362 | 0.0561 |
| T2–T1 | 0.0462 | 0.0364 | 0.0324 | 0.0385 | 0.0291 | 0.0320 | 0.0327 | 0.0646 |
| T1–T2 | 0.0315 | 0.0401 | 0.0359 | 0.0354 | 0.0311 | 0.0324 | 0.0332 | 0.0758 |
| Dataset | Wiener | PCA | wPCA | PInverse | wPInverse | Polynomial 2 | Polynomial 3 | Waypoint-R |
|---|---|---|---|---|---|---|---|---|
| N2–M1 | 0.1360 | 0.1181 | 0.1362 | 0.1292 | 0.1314 | 0.1427 | 0.1482 | 0.1419 |
| N2–W1 | 0.0847 | 0.0566 | 0.0576 | 0.0657 | 0.0552 | 0.0553 | 0.0535 | 0.2098 |
| N2–N1 | 0.0880 | 0.0667 | 0.0379 | 0.0747 | 0.0370 | 0.0412 | 0.0393 | 0.1440 |
| N1–N2 | 0.0491 | 0.0530 | 0.0371 | 0.0632 | 0.0385 | 0.0373 | 0.0370 | 0.1182 |
| T2–M1 | 0.2198 | 0.1796 | 0.2853 | 0.2098 | 0.1659 | 0.1913 | 0.2805 | 0.2637 |
| T2–F1 | 0.1458 | 0.1275 | 0.1208 | 0.1471 | 0.1241 | 0.1155 | 0.1208 | 0.2518 |
| T2–W1 | 0.1549 | 0.1647 | 0.1591 | 0.1881 | 0.1688 | 0.1456 | 0.1886 | 0.2708 |
| T2–T1 | 0.2003 | 0.1770 | 0.1277 | 0.1888 | 0.1281 | 0.1225 | 0.1045 | 0.2637 |
| T1–T2 | 0.0923 | 0.1115 | 0.0942 | 0.1184 | 0.0920 | 0.1148 | 0.1084 | 0.2713 |
| Dataset | Wiener | PCA | wPCA | PInverse | wPInverse | Polynomial 2 | Polynomial 3 | Waypoint-R |
|---|---|---|---|---|---|---|---|---|
| N2–M1 | 1.04 (2.62) | 0.84 (2.31) | 0.91 (1.78) | 0.93 (2.49) | 0.93 (1.9) | 1.02 (1.95) | 1.03 (1.73) | 0.90 (2) |
| N2–W1 | 0.57 (1.77) | 0.33 (1.29) | 0.27 (1.16) | 0.30 (1.29) | 0.20 (0.7) | 0.23 (0.86) | 0.22 (0.84) | 0.83 (2.99) |
| N2–N1 | 0.5 (1.65) | 0.31 (1.23) | 0.17 (0.7) | 0.31 (1.42) | 0.16 (0.55) | 0.17 (0.43) | 0.14 (0.4) | 0.83 (1.86) |
| N1–N2 | 0.32 (1.27) | 0.3 (0.96) | 0.15 (0.65) | 0.28 (1.06) | 0.15 (0.47) | 0.16 (0.58) | 0.14 (0.57) | 0.76 (1.77) |
| T2–M1 | 1.12 (3.78) | 1 (3.68) | 0.92 (3.04) | 1.03 (3.7) | 0.88 (2.63) | 0.98 (2.94) | 0.93 (2.52) | 0.86 (3.12) |
| T2–F1 | 1.15 (4.23) | 1.09 (3.2) | 0.73 (2.32) | 0.89 (3.91) | 0.64 (2.25) | 0.67 (2.12) | 0.61 (1.99) | 0.77 (2.69) |
| T2–W1 | 0.86 (3.79) | 0.95 (3.14) | 0.73 (2.52) | 0.80 (3.46) | 0.63 (2.03) | 0.61 (2.06) | 0.65 (2.23) | 0.99 (3.93) |
| T2–T1 | 0.87 (3.56) | 0.79 (2.96) | 0.47 (1.68) | 0.75 (3.2) | 0.44 (1.51) | 0.48 (1.85) | 0.44 (1.37) | 0.86 (3.12) |
| T1–T2 | 0.63 (3.23) | 0.81 (2.66) | 0.5 (1.22) | 0.65 (2.95) | 0.47 (1.51) | 0.44 (1.57) | 0.43 (1.51) | 0.76 (2.77) |
| Dataset | Wiener | PCA | wPCA | PInverse | wPInverse | Polynomial 2 | Polynomial 3 | Waypoint-R |
|---|---|---|---|---|---|---|---|---|
| N2–M1 | 2.83 (6.43) | 2.26 (5.97) | 2.39 (5.01) | 2.50 (6.11) | 2.48 (5.15) | 2.72 (5.07) | 2.74 (4.94) | 2.35 (5.13) |
| N2–W1 | 1.66 (5.62) | 0.93 (3.84) | 0.73 (3.27) | 0.86 (4.62) | 0.54 (1.85) | 0.57 (2.25) | 0.57 (2.14) | 2.31 (8.9) |
| N2–N1 | 1.61 (5.77) | 0.92 (4.21) | 0.51 (2.21) | 0.92 (4.93) | 0.47 (1.92) | 0.49 (1.25) | 0.42 (1.22) | 2.20 (5.29) |
| N1–N2 | 1 (4.47) | 0.87 (3.22) | 0.44 (2.04) | 0.81 (3.71) | 0.42 (1.4) | 0.45 (1.75) | 0.40 (1.73) | 1.99 (4.95) |
| T2–M1 | 2.61 (11.35) | 2.4 (11.16) | 2.05 (9.04) | 2.43 (11.07) | 1.93 (7.19) | 2.25 (8.87) | 2.14 (6.84) | 1.78 (7.75) |
| T2–F1 | 2.62 (12.57) | 2.79 (8.8) | 1.78 (5.63) | 2.06 (11.37) | 1.34 (5.31) | 1.49 (4.77) | 1.34 (4.24) | 1.48 (6.97) |
| T2–W1 | 2.1 (11.31) | 2.47 (8.86) | 1.89 (7.24) | 1.98 (10.21) | 1.54 (5.72) | 1.41 (4.85) | 1.64 (6.87) | 2.47 (10.5) |
| T2–T1 | 2.54 (10.35) | 2.11 (8.28) | 1.21(4.51) | 2.04 (9.74) | 1.11 (3.54) | 1.23 (3.73) | 1.12 (3.3) | 1.78 (7.75) |
| T1–T2 | 1.65 (10.27) | 2.19 (8.05) | 1.37 (3.45) | 1.75 (9.28) | 1.26 (3.38) | 1.18 (3.89) | 1.14 (3.22) | 1.57 (6.94) |
| Dataset | Wiener | PCA | wPCA | PInverse | wPInverse | Polynomial 2 | Polynomial 3 | Waypoint-R |
|---|---|---|---|---|---|---|---|---|
| N2–M1 | 1.78 (7.93) | 1.52 (7.49) | 1.49 (5.4) | 1.66 (7.83) | 1.60 (5.72) | 1.57 (5.44) | 1.82 (5.75) | 1.51 (7.32) |
| N2–W1 | 1.23 (6.28) | 1.23 (4.43) | 1.07 (3.76) | 1.11 (5.39) | 0.87 (3.9) | 0.96 (3.82) | 0.94 (3.71) | 1.94 (10.71) |
| N2–N1 | 1.43 (7.68) | 1.03 (5.57) | 0.61 (3.29) | 1.01 (6.61) | 0.58 (3.04) | 0.59 (2.79) | 0.52 (1.64) | 0.98 (5.42) |
| N1–N2 | 2.01 (6.41) | 0.91 (4.18) | 0.57 (1.73) | 1.01 (5.16) | 0.57 (1.63) | 0.62 (1.86) | 0.54 (1.41) | 1.22 (4.15) |
| T2–M1 | 3.12 (16.83) | 2.89 (16.12) | 2.80 (13.43) | 3.03 (16.73) | 2.73 (13.53) | 3.14 (13.82) | 2.99 (12.77) | 3.00 (13.92) |
| T2–F1 | 1.90 (15.95) | 1.79 (12) | 1.82 (7.83) | 1.70 (14.98) | 1.19 (9.07) | 1.63 (8.37) | 1.62 (7.83) | 1.84 (13.92) |
| T2–W1 | 3.35 (15.58) | 2.90 (13.01) | 2.39 (10.19) | 2.71 (14.54) | 2.17 (10.07) | 2.48 (10.18) | 2.26 (9.82) | 3.17 (14.92) |
| T2–T1 | 3.75 (15.13) | 2.88 (12.99) | 2.22 (8.12) | 3.11 (14.65) | 2.23 (8.13) | 2.31 (7.82) | 2.06 (8.45) | 2.80 (12.01) |
| T1–T2 | 2.93 (12.69) | 3.14 (10.15) | 2.37 (5.56) | 2.36 (11.88) | 2.17 (4.9) | 2.24 (5.61) | 2.08 (6.4) | 2.11 (7.14) |
| Dataset | Wiener | PCA | wPCA | PInverse | wPInverse | Polynomial 2 | Polynomial 3 | Waypoint-R |
|---|---|---|---|---|---|---|---|---|
| N2–M1 | 2.65 (6.46) | 2.44 (6.18) | 2.39 (4.95) | 2.39 (6.17) | 2.38 (4.62) | 2.61 (4.82) | 2.61 (4.54) | 2.14 (4.95) |
| N2–W1 | 1.55 (6.17) | 1.01 (4.16) | 0.80 (3.11) | 0.94 (5.19) | 0.61 (2.07) | 0.64 (2.14) | 0.64 (2.03) | 2.40 (8.44) |
| N2–N1 | 1.59 (6.39) | 0.93 (4.63) | 0.49 (2.37) | 0.95 (5.45) | 0.45 (2.09) | 0.46 (1.36) | 0.39 (1.2) | 1.77 (4.22) |
| N1–N2 | 1.24 (5.06) | 0.88 (3.57) | 0.43 (1.93) | 0.88 (4.17) | 0.43 (1.29) | 0.43 (1.77) | 0.38 (1.6) | 1.51 (3.43) |
| T2–M1 | 3.29 (11.56) | 3.27 (11.29) | 2.97 (8.84) | 3.21 (11.25) | 2.75 (7.1) | 3.00 (8.92) | 2.83 (6.71) | 2.65 (6.87) |
| T2–F1 | 2.74 (13.21) | 3.08 (9.04) | 2.14 (6.76) | 2.33 (12.1) | 1.65 (5.59) | 1.81 (4.4) | 1.67 (4.59) | 1.95 (6.88) |
| T2–W1 | 2.45 (12) | 2.90 (9.29) | 2.33 (8.88) | 2.42 (10.93) | 1.95 (7.48) | 1.83 (4.59) | 1.99 (8.32) | 2.76 (9.58) |
| T2–T1 | 4.11 (12.2) | 2.63 (9.31) | 1.67 (7.21) | 3.04 (11.29) | 1.84 (6.63) | 1.64 (4.42) | 1.52 (4.73) | 2.40 (8.33) |
| T1–T2 | 2.20 (11.76) | 2.56 (8.82) | 1.81 (4.24) | 2.12 (10.66) | 1.66 (4.09) | 1.68 (4.9) | 1.66 (4.44) | 2.37 (6.35) |
| D50 | D65 | A | F11 | LED-V1 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D65 | A | F11 | D50 | A | F11 | D50 | D65 | F11 | D50 | D65 | A | D50 | D65 | A | ||
| Reference | 1.35 | 2.88 | 1.72 | 1.33 | 4.05 | 2.61 | 2.88 | 4.09 | 2.32 | 1.24 | 1.68 | 3.18 | 2.67 | 3.9 | 0.35 | |
| Waypoint-R | 1.36 | 2.83 | 1.53 | 1.34 | 4 | 2.51 | 2.84 | 4.06 | 2.04 | 1.12 | 1.54 | 3.05 | 2.63 | 3.85 | 0.36 | |
| Burns-CAT | 1.35 | 2.79 | 1.74 | 1.37 | 4.11 | 3.11 | 2.66 | 3.89 | 1.04 | 0.78 | 1.71 | 1.31 | 1.98 | 2.86 | 0.2 | |
| M1–M1 | Burns-R | 1.45 | 2.88 | 1.57 | 1.44 | 4.22 | 2.36 | 2.72 | 4.02 | 2.41 | 1.47 | 1.74 | 3.72 | 2.42 | 3.77 | 0.26 |
| wPInverse | 1.35 | 2.79 | 1.43 | 1.33 | 3.97 | 2.38 | 2.78 | 3.99 | 2.12 | 1.07 | 1.41 | 3.08 | 2.59 | 3.83 | 0.33 | |
| Polynomial 3 | 1.35 | 2.84 | 1.57 | 1.33 | 4.01 | 2.41 | 2.84 | 4.06 | 2.24 | 1.26 | 1.57 | 3.21 | 2.56 | 3.81 | 0.36 | |
| F1–F1 | Reference | 1.68 | 3.50 | 2.54 | 1.68 | 5.07 | 3.74 | 3.50 | 5.07 | 2.15 | 2.08 | 2.98 | 3.10 | 3.77 | 5.29 | 1.05 |
| Reference | 1.70 | 3.32 | 2.56 | 1.70 | 4.94 | 3.78 | 3.32 | 4.94 | 2.39 | 1.98 | 2.96 | 3.40 | 3.69 | 5.11 | 1.48 | |
| T2–T2 | Burns-CAT | 1.49 | 2.9 | 1.86 | 1.5 | 4.37 | 3.35 | 2.79 | 4.23 | 1.01 | 0.96 | 2.14 | 1.57 | 2.32 | 3.45 | 0.17 |
| Burns-R | 1.73 | 3.19 | 1.52 | 1.71 | 4.83 | 2.72 | 3.13 | 4.83 | 2.6 | 1.45 | 1.68 | 4.04 | 2.54 | 4.01 | 0.27 | |
| Waypoint-R | 1.57 | 2.9 | 1.61 | 1.56 | 4.4 | 2.75 | 2.88 | 4.4 | 2 | 1.13 | 1.56 | 3.18 | 2.56 | 3.85 | 0.40 | |
| T2–F1 | wPInverse | 1.65 | 3.39 | 2.60 | 1.65 | 4.94 | 3.70 | 3.43 | 4.96 | 2.07 | 2.85 | 3.31 | 2.92 | 3.47 | 4.86 | 1.11 |
| Polynomial 3 | 1.67 | 3.43 | 2.63 | 1.67 | 5.00 | 3.80 | 3.47 | 5.03 | 2.11 | 2.78 | 3.39 | 2.98 | 3.57 | 4.86 | 1.06 | |
| Waypoint-R | 1.54 | 2.86 | 1.29 | 1.53 | 4.3 | 2.5 | 2.88 | 4.37 | 2.06 | 1.13 | 1.56 | 3.18 | 2.56 | 3.85 | 0.40 | |
| T2–M1 | wPInverse | 1.51 | 2.79 | 1.42 | 1.51 | 4.21 | 2.57 | 2.79 | 4.23 | 2.07 | 1.22 | 1.37 | 3.10 | 2.49 | 3.77 | 0.37 |
| Polynomial 3 | 1.5 | 2.82 | 1.72 | 1.5 | 4.23 | 2.68 | 2.82 | 4.23 | 2.24 | 1.37 | 1.63 | 3.21 | 2.54 | 3.74 | 0.38 | |
| Mean ΔE00 | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D50 | D65 | A | F11 | LED-V1 | ||||||||||||
| D65 | A | F11 | D50 | A | F11 | D50 | D65 | F11 | D50 | D65 | A | D50 | D65 | A | ||
| M1–M1 | CAT02 | 0.59 | 2.01 | 1.87 | 0.61 | 2.63 | 1.92 | 1.89 | 2.37 | 2.63 | 1.93 | 1.99 | 2.66 | 1.98 | 2.45 | 0.56 |
| CAT16 | 0.78 | 2.73 | 1.93 | 0.80 | 3.56 | 2.23 | 2.55 | 3.24 | 2.87 | 2.00 | 2.33 | 2.99 | 2.64 | 3.31 | 0.54 | |
| L-Bradford | 0.52 | 1.74 | 1.93 | 0.53 | 2.25 | 1.98 | 1.73 | 2.18 | 2.35 | 1.99 | 2.07 | 2.32 | 1.69 | 2.11 | 0.55 | |
| Oleari-MAT | 0.61 | 1.77 | 2.49 | 0.59 | 2.13 | 2.24 | 1.84 | 2.28 | 3.16 | 2.44 | 2.20 | 3.01 | — | — | — | |
| Waypoint-MAT | 0.33 | 0.80 | 1.34 | 0.33 | 1.09 | 1.42 | 0.87 | 1.22 | 1.55 | 1.36 | 1.40 | 1.50 | — | — | — | |
| Burns-CAT | 0.55 | 1.73 | 2.03 | 0.56 | 2.28 | 2.23 | 1.73 | 2.25 | 2.43 | 2.05 | 2.24 | 2.36 | 1.90 | 2.39 | 0.55 | |
| Burns-R | 0.27 | 0.68 | 1.22 | 0.26 | 0.92 | 1.21 | 0.82 | 1.14 | 1.66 | 1.42 | 1.44 | 1.57 | 0.72 | 0.96 | 0.34 | |
| wPInverse | 0.19 | 0.49 | 0.87 | 0.19 | 0.66 | 0.94 | 0.53 | 0.74 | 0.92 | 0.89 | 0.95 | 0.86 | 0.49 | 0.66 | 0.2 | |
| Polynomial 3 | 0.21 | 0.54 | 0.98 | 0.2 | 0.73 | 1.05 | 0.58 | 0.79 | 1.06 | 0.97 | 1.05 | 1.01 | 0.54 | 0.72 | 0.23 | |
| 95th Percentile ΔE00 | ||||||||||||||||
| M1-M1 | CAT02 | 1.37 | 4.48 | 5.08 | 1.41 | 6.06 | 5.34 | 4.04 | 5.26 | 5.54 | 5.32 | 5.56 | 5.75 | 4.55 | 5.61 | 1.24 |
| CAT16 | 1.69 | 5.77 | 5.24 | 1.71 | 7.66 | 5.78 | 5.35 | 6.93 | 5.98 | 5.50 | 6.13 | 6.54 | 5.89 | 7.36 | 1.23 | |
| L-Bradford | 1.20 | 3.56 | 5.25 | 1.22 | 4.85 | 5.44 | 3.48 | 4.54 | 5.18 | 5.37 | 5.62 | 5.12 | 3.69 | 4.69 | 1.23 | |
| Oleari-MAT | 1.18 | 3.20 | 4.71 | 1.12 | 4.04 | 4.50 | 3.52 | 4.79 | 7.59 | 4.47 | 4.49 | 6.02 | — | — | — | |
| Waypoint-MAT | 1.10 | 2.63 | 3.82 | 1.05 | 3.53 | 3.95 | 2.87 | 4.06 | 4.79 | 3.77 | 3.91 | 4.72 | — | — | — | |
| Burns-CAT | 1.37 | 4.34 | 5.03 | 1.37 | 5.68 | 5.37 | 4.41 | 5.70 | 5.45 | 5.12 | 5.48 | 5.24 | 4.98 | 6.38 | 1.25 | |
| Burns-R | 0.65 | 1.75 | 3.43 | 0.60 | 2.26 | 3.09 | 2.20 | 3.01 | 5.03 | 3.63 | 3.72 | 3.80 | 1.89 | 2.61 | 0.86 | |
| wPInverse | 0.48 | 1.32 | 2.48 | 0.47 | 1.71 | 2.69 | 1.38 | 1.90 | 2.91 | 2.49 | 2.68 | 2.57 | 1.23 | 1.72 | 0.46 | |
| Polynomial 3 | 0.62 | 1.69 | 2.47 | 0.64 | 2.28 | 2.82 | 1.74 | 2.39 | 2.81 | 2.40 | 2.75 | 2.57 | 1.52 | 2.09 | 0.67 | |
| Mean ΔE00 | 95th percentile of ΔE00 | |||
|---|---|---|---|---|
| Method | A-D65 | F11-D65 | A-D65 | F11-D65 |
| Centroid method (Zhang et al.) | 1.27 | 1.82 | 3.42 | 4.99 |
| wPInverse (M1–M1) | 0.74 | 0.95 | 1.90 | 2.68 |
| Polynomial 3 (M1–M1) | 0.79 | 1.05 | 2.39 | 2.75 |
| D50 | D65 | A | F11 | LED-V1 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D65 | A | F11 | D50 | A | F11 | D50 | D65 | F11 | D50 | D65 | A | D50 | D65 | A | Avg | ||
| N2-N2 | CAT02 | 0.96 | 2.59 | 1.77 | 0.95 | 3.47 | 2.03 | 2.78 | 3.76 | 2.70 | 1.81 | 2.07 | 2.58 | 2.47 | 3.28 | 1.15 | 2.29 |
| CAT16 | 1.02 | 2.83 | 1.87 | 1.01 | 3.76 | 2.25 | 2.97 | 4.01 | 2.70 | 1.92 | 2.32 | 2.62 | 2.69 | 3.56 | 1.17 | 2.45 | |
| L-Bradford | 0.93 | 2.38 | 1.81 | 0.91 | 3.21 | 2.10 | 2.62 | 3.60 | 2.53 | 1.85 | 2.16 | 2.38 | 2.20 | 3.00 | 1.14 | 2.19 | |
| Oleari-MAT | 0.53 | 1.75 | 2.54 | 0.53 | 1.98 | 2.79 | 1.76 | 1.99 | 1.45 | 2.57 | 2.78 | 1.56 | — | — | — | 1.85 | |
| Waypoint-MAT | 0.92 | 2.37 | 1.32 | 0.90 | 3.19 | 1.73 | 2.62 | 3.63 | 2.47 | 1.30 | 1.68 | 2.13 | — | — | — | 2.02 | |
| Burns-CAT | 0.96 | 2.61 | 1.85 | 0.94 | 3.46 | 2.22 | 2.83 | 3.85 | 2.58 | 1.87 | 2.25 | 2.45 | 2.52 | 3.34 | 1.11 | 2.32 | |
| Burns-R | 0.80 | 2.10 | 1.20 | 0.79 | 2.79 | 1.65 | 2.29 | 3.17 | 1.95 | 1.66 | 2.07 | 1.90 | 1.76 | 2.37 | 1.10 | 1.84 | |
| wPInverse | 0.11 | 0.34 | 0.37 | 0.11 | 0.45 | 0.46 | 0.37 | 0.48 | 0.26 | 0.39 | 0.47 | 0.25 | 0.36 | 0.46 | 0.08 | 0.33 | |
| Polynomial 3 | 0.1 | 0.29 | 0.33 | 0.1 | 0.38 | 0.42 | 0.32 | 0.42 | 0.2 | 0.35 | 0.43 | 0.2 | 0.31 | 0.4 | 0.04 | 0.29 | |
| N2-M1 | wPInverse | 0.78 | 2.11 | 1.18 | 0.77 | 2.81 | 1.33 | 2.31 | 3.16 | 2.46 | 1.18 | 1.33 | 2.14 | 1.82 | 2.47 | 1.01 | 1.79 |
| Polynomial 3 | 0.87 | 2.34 | 1.32 | 0.85 | 3.14 | 1.48 | 2.55 | 3.48 | 2.96 | 1.28 | 1.43 | 2.52 | 2.00 | 2.71 | 1.13 | 2.00 | |
| N2-W1 | wPInverse | 0.18 | 0.48 | 0.74 | 0.17 | 0.65 | 0.79 | 0.52 | 0.70 | 0.78 | 0.77 | 0.80 | 0.77 | 0.52 | 0.64 | 0.25 | 0.58 |
| Polynomial 3 | 0.20 | 0.54 | 0.81 | 0.20 | 0.72 | 0.88 | 0.58 | 0.78 | 0.79 | 0.83 | 0.86 | 0.79 | 0.56 | 0.70 | 0.25 | 0.63 | |
| N2-N1 | wPInverse | 0.14 | 0.41 | 0.49 | 0.14 | 0.54 | 0.56 | 0.44 | 0.58 | 0.49 | 0.52 | 0.57 | 0.50 | 0.40 | 0.52 | 0.12 | 0.43 |
| Polynomial 3 | 0.13 | 0.39 | 0.44 | 0.13 | 0.52 | 0.49 | 0.43 | 0.56 | 0.51 | 0.46 | 0.5 | 0.51 | 0.37 | 0.49 | 0.11 | 0.40 | |
| D50 | D65 | A | F11 | LED-V1 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D65 | A | F11 | D50 | A | F11 | D50 | D65 | F11 | D50 | D65 | A | D50 | D65 | A | Avg | ||
| N2-N2 | CAT02 | 1.91 | 4.57 | 4.67 | 1.83 | 5.92 | 5.16 | 5.29 | 7.20 | 6.32 | 4.97 | 5.84 | 5.68 | 4.84 | 6.55 | 2.36 | 4.87 |
| CAT16 | 1.81 | 5.09 | 4.84 | 1.73 | 6.77 | 5.60 | 5.26 | 6.97 | 6.12 | 5.20 | 6.50 | 5.76 | 6.21 | 7.63 | 2.34 | 5.19 | |
| L-Bradford | 1.80 | 4.54 | 4.78 | 1.75 | 5.87 | 5.38 | 5.30 | 6.99 | 5.43 | 5.10 | 6.18 | 4.78 | 4.32 | 6.15 | 2.36 | 4.72 | |
| Oleari-MAT | 1.24 | 3.79 | 5.14 | 1.18 | 4.85 | 5.93 | 3.89 | 4.96 | 3.52 | 5.30 | 5.93 | 3.12 | — | — | — | 4.07 | |
| Waypoint-MAT | 1.78 | 4.78 | 3.84 | 1.72 | 6.30 | 4.69 | 5.32 | 7.33 | 7.80 | 3.65 | 4.61 | 6.65 | — | — | — | 4.87 | |
| Burns-CAT | 1.79 | 4.64 | 4.96 | 1.71 | 6.18 | 5.60 | 5.19 | 6.89 | 6.49 | 5.34 | 6.65 | 6.13 | 5.31 | 6.80 | 2.36 | 5.07 | |
| Burns-R | 1.74 | 4.71 | 3.41 | 1.75 | 6.10 | 4.68 | 5.09 | 6.74 | 4.09 | 4.70 | 5.46 | 3.66 | 4.11 | 5.42 | 2.29 | 4.26 | |
| wPInverse | 0.62 | 1.69 | 2.26 | 0.63 | 2.26 | 2.69 | 1.97 | 2.53 | 1.14 | 2.39 | 2.65 | 1.12 | 1.74 | 2.29 | 0.48 | 1.76 | |
| Polynomial 3 | 0.72 | 2.02 | 1.97 | 0.75 | 2.66 | 2.65 | 2.43 | 3.03 | 0.99 | 2.20 | 2.72 | 0.89 | 2.27 | 2.88 | 0.20 | 1.89 | |
| N2–M1 | wPInverse | 1.75 | 4.77 | 3.23 | 1.69 | 6.23 | 4.31 | 5.32 | 7.15 | 6.94 | 3.13 | 4.03 | 5.59 | 4.52 | 6.04 | 2.14 | 4.46 |
| Polynomial 3 | 1.93 | 5.33 | 3.74 | 1.90 | 7.07 | 4.62 | 5.89 | 7.82 | 7.69 | 3.66 | 4.31 | 5.75 | 4.95 | 6.70 | 2.28 | 4.91 | |
| N2–W1 | wPInverse | 0.93 | 2.60 | 2.70 | 1.09 | 3.67 | 4.27 | 2.14 | 3.06 | 2.43 | 2.40 | 2.81 | 2.46 | 2.08 | 2.71 | 0.99 | 2.42 |
| Polynomial 3 | 1.04 | 2.68 | 3.08 | 1.03 | 3.49 | 3.96 | 3.27 | 4.23 | 2.40 | 3.43 | 4.21 | 2.40 | 3.04 | 4.00 | 0.91 | 2.88 | |
| N2–N1 | wPInverse | 0.58 | 1.76 | 2.01 | 0.57 | 2.31 | 2.52 | 1.94 | 2.44 | 1.52 | 2.18 | 2.62 | 1.54 | 1.85 | 2.27 | 0.42 | 1.77 |
| Polynomial 3 | 0.57 | 1.61 | 2.17 | 0.58 | 2.10 | 2.69 | 1.91 | 2.41 | 1.55 | 2.36 | 2.71 | 1.53 | 1.85 | 2.35 | 0.38 | 1.78 | |
| D50 | D65 | A | F11 | LED-V1 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D65 | A | F11 | D50 | A | F11 | D50 | D65 | F11 | D50 | D65 | A | D50 | D65 | A | Avg | ||
| T2–T2 | CAT02 | 0.84 | 2.32 | 2.91 | 0.83 | 3.11 | 3.31 | 2.32 | 3.11 | 2.83 | 3.01 | 3.46 | 2.76 | 2.58 | 3.16 | 1.67 | 2.55 |
| CAT16 | 0.98 | 2.84 | 2.99 | 0.98 | 3.78 | 3.53 | 2.82 | 3.76 | 2.86 | 3.12 | 3.77 | 2.82 | 2.98 | 3.67 | 1.68 | 2.84 | |
| L-Bradford | 0.80 | 2.03 | 2.96 | 0.79 | 2.75 | 3.37 | 2.15 | 2.94 | 2.51 | 3.07 | 3.55 | 2.42 | 2.17 | 2.68 | 1.66 | 2.39 | |
| Oleari-MAT | 0.61 | 1.82 | 3.38 | 0.60 | 2.18 | 3.61 | 1.82 | 2.21 | 2.69 | 3.40 | 3.61 | 2.85 | — | — | — | 2.40 | |
| Waypoint-MAT | 0.74 | 1.66 | 2.15 | 0.72 | 2.31 | 2.67 | 1.82 | 2.61 | 1.87 | 2.12 | 2.62 | 1.77 | — | — | — | 1.92 | |
| Burns-CAT | 0.86 | 2.30 | 3.12 | 0.85 | 3.09 | 3.70 | 2.42 | 3.32 | 2.50 | 3.21 | 3.92 | 2.36 | 2.64 | 3.21 | 1.63 | 2.61 | |
| Burns-R | 0.72 | 1.46 | 2.14 | 0.68 | 2.04 | 2.57 | 1.67 | 2.47 | 1.52 | 2.41 | 2.96 | 1.58 | 1.67 | 1.93 | 1.66 | 1.83 | |
| wPInverse | 0.24 | 0.58 | 0.89 | 0.24 | 0.80 | 1.10 | 0.64 | 0.90 | 0.50 | 0.95 | 1.15 | 0.53 | 0.64 | 0.85 | 0.28 | 0.69 | |
| Polynomial 3 | 0.25 | 0.59 | 1.02 | 0.24 | 0.81 | 1.20 | 0.68 | 0.95 | 0.66 | 1.16 | 1.38 | 0.70 | 0.63 | 0.88 | 0.16 | 0.75 | |
| T2–M1 | wPInverse | 0.58 | 1.30 | 1.73 | 0.56 | 1.81 | 2.12 | 1.42 | 2.03 | 1.44 | 1.77 | 2.15 | 1.44 | 1.59 | 1.92 | 1.37 | 1.55 |
| Polynomial 3 | 0.62 | 1.47 | 1.87 | 0.61 | 2.03 | 2.24 | 1.60 | 2.25 | 1.69 | 1.92 | 2.30 | 1.66 | 1.66 | 2.02 | 1.40 | 1.69 | |
| T2–F1 | wPInverse | 0.41 | 0.94 | 1.32 | 0.41 | 1.31 | 1.58 | 1.03 | 1.44 | 1.07 | 1.39 | 1.65 | 1.05 | 1.13 | 1.38 | 0.76 | 1.12 |
| Polynomial 3 | 0.45 | 1.12 | 1.56 | 0.45 | 1.52 | 1.87 | 1.21 | 1.64 | 1.06 | 1.63 | 1.93 | 1.05 | 1.37 | 1.63 | 0.76 | 1.28 | |
| T2–T1 | wPInverse | 0.30 | 0.74 | 1.43 | 0.29 | 0.99 | 1.62 | 0.85 | 1.18 | 1.16 | 1.51 | 1.7 | 1.2 | 1.28 | 1.54 | 0.77 | 1.10 |
| Polynomial 3 | 0.30 | 0.77 | 1.39 | 0.29 | 1.02 | 1.58 | 0.91 | 1.25 | 1.09 | 1.56 | 1.79 | 1.13 | 1.11 | 1.42 | 0.53 | 1.08 | |
| D50 | D65 | A | F11 | LED-V1 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D65 | A | F11 | D50 | A | F11 | D50 | D65 | F11 | D50 | D65 | A | D50 | D65 | A | Avg | ||
| T2–T1 | CAT02 | 2.66 | 5.50 | 9.81 | 2.59 | 7.57 | 10.11 | 6.37 | 9.21 | 8.47 | 10.43 | 11.37 | 7.56 | 5.89 | 7.79 | 5.39 | 7.38 |
| CAT16 | 2.59 | 6.92 | 10.11 | 2.50 | 9.18 | 10.78 | 6.49 | 9.05 | 8.06 | 11.02 | 12.47 | 7.26 | 7.74 | 9.70 | 5.38 | 7.95 | |
| L-Bradford | 2.61 | 5.05 | 9.93 | 2.54 | 7.26 | 10.34 | 6.05 | 9.15 | 8.06 | 10.56 | 11.73 | 7.29 | 4.93 | 7.31 | 5.39 | 7.21 | |
| Oleari-MAT | 2.10 | 5.90 | 8.89 | 2.03 | 7.99 | 10.61 | 5.87 | 8.03 | 5.68 | 8.76 | 10.41 | 6.25 | — | — | — | 6.88 | |
| Waypoint-MAT | 2.58 | 5.73 | 8.65 | 2.54 | 7.86 | 10.29 | 6.69 | 9.77 | 10.47 | 8.15 | 10.04 | 9.41 | — | — | — | 7.68 | |
| Burns-CAT | 2.57 | 5.78 | 10.58 | 2.48 | 7.65 | 11.56 | 6.20 | 9.01 | 7.62 | 11.51 | 13.42 | 6.41 | 6.78 | 8.54 | 5.39 | 7.70 | |
| Burns-R | 2.45 | 5.19 | 6.72 | 2.40 | 7.20 | 8.85 | 5.90 | 8.60 | 5.63 | 8.43 | 10.33 | 5.50 | 4.92 | 6.42 | 5.33 | 6.26 | |
| wPInverse | 1.29 | 2.55 | 3.92 | 1.35 | 3.85 | 5.24 | 3.1 | 4.68 | 1.88 | 3.87 | 5.24 | 2.16 | 3.17 | 4.84 | 1.02 | 3.21 | |
| Polynomial 3 | 1.08 | 2.41 | 4.17 | 1.05 | 3.46 | 5.28 | 2.99 | 4.25 | 2.51 | 4.39 | 5.29 | 2.36 | 2.8 | 4.11 | 0.75 | 3.13 | |
| T2–M1 | wPInverse | 2.54 | 5.57 | 7.26 | 2.49 | 7.61 | 8.36 | 6.47 | 9.16 | 7.24 | 7.18 | 8.77 | 6.28 | 4.74 | 7.11 | 4.84 | 6.37 |
| Polynomial 3 | 2.76 | 6.22 | 6.23 | 2.71 | 8.53 | 8.72 | 7.06 | 9.77 | 7.16 | 6.21 | 8.33 | 5.65 | 5.21 | 7.78 | 4.71 | 6.47 | |
| T2-F1 | wPInverse | 1.69 | 2.95 | 5.11 | 1.68 | 4.26 | 6.12 | 3.43 | 5.36 | 2.72 | 5.4 | 6.72 | 3.18 | 3.64 | 3.87 | 4.08 | 4.01 |
| Polynomial 3 | 1.56 | 3.65 | 4.92 | 1.46 | 4.74 | 5.89 | 4.2 | 5.41 | 2.52 | 4.89 | 5.78 | 2.62 | 4.71 | 5.99 | 4.08 | 4.16 | |
| T2-T1 | wPInverse | 1.46 | 3.07 | 5.25 | 1.41 | 4.23 | 6.63 | 3.99 | 5.74 | 3.60 | 5.53 | 7.05 | 3.59 | 4.51 | 6.34 | 2.05 | 4.30 |
| Polynomial 3 | 1.51 | 3.13 | 5.31 | 1.38 | 4.19 | 6.60 | 4.11 | 5.79 | 3.02 | 5.97 | 7.52 | 3.50 | 4.12 | 5.89 | 1.86 | 4.26 | |
| Method | Mean | Median | 95 Percentile | Maximum |
|---|---|---|---|---|
| wPInverse | 0.85 | 0.71 | 2.04 | 3.62 |
| Polynomial 3 | 0.89 | 0.72 | 2.24 | 3.83 |
| Method | CSAJ | Helson | Lam & Rigg | Lutchi | Average |
|---|---|---|---|---|---|
| Cat02 | 3.67 | 3.60 | 2.98 | 3.41 | 3.42 |
| Cat16 | 3.94 | 4.13 | 3.47 | 3.30 | 3.71 |
| L-Bradford | 3.71 | 3.47 | 2.84 | 3.43 | 3.36 |
| Burns-CAT | 3.81 | 4.19 | 3.15 | 3.68 | 3.71 |
| Oleari-MAT | 4.63 | 4.72 | 3.89 | 4.27 | 4.38 |
| Wpt-MAT | 4.28 | 4.02 | 3.83 | 4.53 | 4.17 |
| wPInverse(M1) | 4.14 | 3.76 | 3.48 | 4.51 | 3.97 |
| Polynomial 3 (M1) | 4.22 | 3.77 | 3.51 | 4.46 | 3.99 |
| wPInverse (N2) | 4.71 | 3.65 | 3.42 | 4.29 | 4.02 |
| Polynomial 3 (N2) | 4.39 | 3.76 | 3.47 | 4.34 | 3.99 |
| wPInverse (T2) | 4.69 | 3.65 | 3.46 | 4.36 | 4.04 |
| Polynomial 3 (T2) | 4.35 | 3.57 | 3.31 | 4.37 | 3.90 |
 Find this author on Google Scholar
Find this author on Google Scholar Find this author on PubMed
Find this author on PubMed
 Open access
Open access