Matrix R-based Visual Response to Optimal Colors and Application to Image Color Gamut Expansion

Hiroaki Kotera

doi:10.2352/J.ImagingSci.Technol.2023.67.5.050414

Abstract

The optimal colors with maximum chroma at constant lightness present an ideal target for the colorants pursuing the ultimate wide color gamut. MacAdam proved that optimal colors are composed of square pulse-shaped spectra with at least two tansition wavelengths λ₁ and λ₂ whose reflectances change from 0 to 1 or 1 to 0. The optimal color gamut is created from two-types, a convex-type with reflectance 1.0 in w = λ₁ ∼ λ₂ and 0.0 otherwise, or a concave-type with reflectance 0.0 in w = λ₁ ∼ λ₂ and 1.0 otherwise. It takes a high computation cost to search the optimal color candidates in high precision and to create the 3D color gamut. In addition, the human visual spectral responses to the optimal color spectra remain unknown. This paper (1) proposes an alternative simple method for creating the optimal color gamut with GBD (Gamujt Boundary Descriptor) technique, and (2) clarifies how human vision spectrally respond to the optimal colors based on Matrix-R theory, for the first time which was unknown until now, and (3) presents centroid-invariant novel color gamut expansion method considering the optimal color as an ideal target and finally apply it to actual low-saturation images to verify its effect.

jist

JIMTE6

Journal of Imaging Science and Technology

J. Imaging Sci. Technol.

1062-3701

1943-3522

Society for Imaging Science and Technology

050414

10.2352/J.ImagingSci.Technol.2023.67.5.050414

1522

Work Presented at CIC31: Color and Imaging 2023

Matrix R-based Visual Response to Optimal Colors and Application to Image Color Gamut Expansion

Matrix R-based visual response to optimal colors and application to image color gamut expansion

KoteraHiroaki

▴

Kotera Imaging Laboratory, Chiba, Japan

hiroimage@gmail.com

Kotera

▴

IS&T Member.

092023

3052023

192023

2023

Abstract

The optimal colors with maximum chroma at constant lightness present an ideal target for the colorants pursuing the ultimate wide color gamut. MacAdam proved that optimal colors are composed of square pulse-shaped spectra with at least two tansition wavelengths λ1 and λ2 whose reflectances change from 0 to 1 or 1 to 0. The optimal color gamut is created from two-types, a convex-type with reflectance 1.0 in w = λ1 ∼ λ2 and 0.0 otherwise, or a concave-type with reflectance 0.0 in w = λ1 ∼ λ2 and 1.0 otherwise. It takes a high computation cost to search the optimal color candidates in high precision and to create the 3D color gamut. In addition, the human visual spectral responses to the optimal color spectra remain unknown. This paper (1) proposes an alternative simple method for creating the optimal color gamut with GBD (Gamujt Boundary Descriptor) technique, and (2) clarifies how human vision spectrally respond to the optimal colors based on Matrix-R theory, for the first time which was unknown until now, and (3) presents centroid-invariant novel color gamut expansion method considering the optimal color as an ideal target and finally apply it to actual low-saturation images to verify its effect.

ccc

1062-3701/2023/67(5)/050414/13/$25.00

printed

Printed in the USA

Introduction

The idea of optimal colors was first introduced by Ostwald. Schrödinger [1], a famous Nobel Prize winner, and predicted the optimal color pigments with highest luminosity at constant chromaticity, where the spectral reflectances must have at most two transitions between 0 and 1. Thus, two types of “optimal color” spectral reflectances are possible; either the transition goes to 1 in the middle from 0 at the both ends of spectral range (Convex-type), or goes to 0 in the middle from 1 at the both ends conversely (Concave-type). Dyes or pigments with rectangular pulse wave-like spectral distribution do not exist, and such virtual dye is called “block dye” [2]. The optimal color presents an ideal target for developing the colorants with the wider color gamut.

MacAdam [3] gave the first complete proof of the optimal color theorem and the precise coordinates on the boundary of the optimal color solid which is called MacAdam limits. West and Brill [4] generalized the mathematical conditions under which reflectance functions are optimal. MacAdam limits are useful for evaluating the colorimetric reproducibility of the real colorants. Perales et al. [5] searched the optimal colors with 0.1 nm step and succeeded in the formation of high precision optimal color gamut. Fu Jiang et al. [6] estimated the number of discernible object colors from block dye spectral reflectances with 0.1 nm step based on color appearance model CIECAM02.

Although the higher the wavelength resolution, the greater the number of optimal colors seeked out, but it takes high computation cost to create the entire color gamut and makes it hard to compare with that of real colorant quickly. Recently, Contore [7] presented an elegant zonehedral approach to create the optimal color gamut more simpler.

Another motivation in this paper lies in how the human vision responds to the rectangular pulse wave-like block dye spectra with step function. Since the spectral sensitivities of LMS cones have the smoothed band-limited profiles, any dull spectral responses may appear in the human vision when responding to the sharp step functions and may cause the limited chromatic saturation.

This paper discusses afresh the optimal color problem focusing on the following three subjects.

(1)

A simple method for creating the optimal color gamut with GBD (Gamut Boundary Descriptor) used for Gamut Mapping

(2)

How the human vision responds to the rectangular pulse wave-like step function of block dye spectra.

(3)

Application for image gamut expansion aiming at the optimal color gamut as an ideal target.

Figure 1 shows a flow diagram for searching the optimal colors and forming its 3-D color gamut.

Figure 1.

A simple method for forming optimal color gamut with computer generated block dye spectra.

Generation of Block-Dye Spectral Reflectance

The optimal colors come from the two types of spectral color chips as shown in Figure 2.

(A)

Convex-type with reflectance 1.0 in w = λ1 ∼ λ2 and 0.0 otherwise

(B)

Concave-type with reflectance 0.0 in w = λ1 ∼ λ2 and 1.0 otherwise

Assuming the visible wavelength range of 380 nm–730 nm, all possible block dye spectra are generated by changing the two parameters of (λ1, w) as follows.

(1)

λ_{1} = 380 + Δ λ (j - 1) : j = 1 \sim (n - 1) .

The width w is limited to

(2)

w = 730 - λ_{1} = k Δ λ : k = 1 \sim (n - j),

where, n denotes the discrete sampling number as

(3)

n = (730 - 380) ∕ Δ λ + 1 = 350 ∕ Δ λ + 1 .

Since the number of possible shapes for each type in Fig. 2 is given by n(n + 1)∕2, the total number of generated spectra is

(4)

N = n (n + 1) .

Figure 2.

Two types of spectral reflectances for creating optimal colors.

In this paper, the block-dye spectral chips Cm (m = 1 ∼ N) are generated for the two cases of

(a)

Coase: n = 71 dimension, Δλ = 5 nm, N = 5112

(b)

Fine: n = 351 dimension, Δλ = 1 nm, N = 123552

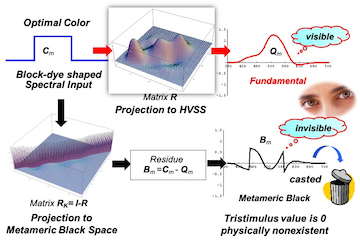
Visual Response to Optimal Color Spectra

Since an optimal color with block-dye shaped spectrum shown in Fig. 2 is a nonexistent ideal colorant, the visual spectral response to such virtual dye is unknown and hasn’t been reported so far.

Though, thinking that a reflective spectrum from a block dye is composed of a set of single spectra contained in the range of w = λ1 ∼ λ2, the visual spectral response to such block dye should be obtained by integrating their single spectral responses.

Now, recall that the Matrix-R [8] is a projection operater to HVSS (Human Visual Sub Space) from specral space. Since the Matrix-R extracts a visible spectrum (called fundamental) from a n-dimensional spectra, we can estimate the visual response to the block dye spectrum. Based on Matrix-R theory, the fundamental Qm, that is, the visual spectral response to a block dye chip Cm is mathematically described by

(5)

\begin{matrix} Q_{m} = R C_{m}, R = A {(A^{t} A)}^{- 1} A^{t} : t = t r a n s p o s e \\ w h e r e, A = [\bar{x} (λ) \bar{y} (λ) \bar{z} (λ)] : c o l o r m a t c h i n g f u n c . \end{matrix}

Here, CIE1964 10 degree color matching function A is used.

Now, input Cm is decomposed to fundamental Qm and the metameric black Bm through the projection operator R as

(6)

C_{m} = Q_{m} + B_{m}, B_{m} = C_{m} - Q_{m} = R_{K} C_{m}, R_{K} = I - R .

Figure 3(a) and (b) illustrate the 3-D profiles of matrix-R for Δλ = 5 nm and Δλ = 1 nm resolutions individualy.

Figure 3.

Matrix R composed of two different wavelength resolution Δλ.

Figure 4 shows a sample how the block dye spectral reflectance is decomposed into the fundamental Qm and the metameric black Bm, where Qm is perceived to human vision as visible spectrum, while Bm, is casted as an invisible component with zero tristimulus value.

Figure 4.

Decomposition of block dye spectrum through Matrix R.

As noticed in the profile of Qm in Figure 5, human vision cannot respond to the sharp spectral change like as step function but shows a dull response.

Figure 5.

Dull human visual spectral response to block dye caused by integrated monochromatic fundamentals gated through block dye pulse.

The fundamental Qm carries the XYZ tristimulus value Tm of block dye spectrum Cm so that the same Tm is obtained even if operating the matrix R on either Cm or Qm over and over again [9]. That is, R means an identity projection operator as follows.

(7)

\begin{matrix} Q_{m} = R Q_{m} = R (R \dots (R Q_{m}) = R^{q} Q_{m} (q = 1 \sim \infty) \\ T_{m} = A^{t} C_{m} = A^{t} Q_{m}, w h i l e T_{B m} = A^{t} B_{m} = 0 . \end{matrix}

Now, describing the Eq. (5) in detail, the visible spectral component Qm is expressed as

(8)

\begin{matrix} Q_{m} = R C_{m} = {[\begin{matrix} u_{1} & u_{2} & u_{3} & \dots \dots \dots & u_{n} \end{matrix}]}^{t} C_{m} \\ = [\begin{matrix} Q_{m} (λ_{1}) \\ Q_{m} (λ_{2}) \\ ⋮ \\ Q_{m} (λ_{j}) \\ ⋮ \\ Q_{m} (λ_{n}) \end{matrix}] \\ = [\begin{matrix} u_{1} (λ_{1}) u_{1} (λ_{2}) u_{1} (λ_{3}) \dots u_{1} (λ_{n}) \\ u_{2} (λ_{1}) u_{2} (λ_{2}) u_{2} (λ_{3}) \dots u_{2} (λ_{n}) \\ ⋮ ⋮ \\ u_{j} (λ_{1}) u_{j} (λ_{2}) u_{j} (λ_{3}) \dots u_{j} (λ_{n}) \\ ⋮ ⋮ \\ u_{n} (λ_{1}) u_{n} (λ_{2}) u_{n} (λ_{3}) \dots u_{n} (λ_{n}) \end{matrix}] [\begin{matrix} C_{m} (λ_{1}) \\ C_{m} (λ_{2}) \\ ⋮ \\ C_{m} (λ_{j}) \\ ⋮ \\ C_{m} (λ_{n}) \end{matrix}] . \end{matrix}

It’s worthy of notice that the fundamentals {uj} corresponding to the monochromatic light stimuli are arranged in each row and column in the Matrix-R. That is, each row vector uj denotes the fundamental to the monochromatic light stimulus Pj whose jth entry is 1.0 alone at the wavelength λj and others are 0.0 as

(9)

\begin{matrix} u_{j} = [u_{j} (λ_{1}) u_{j} (λ_{2}) u_{j} (λ_{3}) \dots u_{j} (λ_{n})] = R P_{j} \\ P_{j} = {[\begin{matrix} 0 & \dots 0 & 1 & 0 \dots 0 \end{matrix}]}^{t} : m o n o c h r o m a t i c s t i m u l u s \\ w i t h j th e n t r y = 1 f o r λ_{j} a n d o t h e r s = 0 . \end{matrix}

Since the Matrix-R is symmetric, there is the following relation between the row and column entries

(10)

u_{j} (k) = u_{k} (j) .

Hence Eq. (8) means that the fundamental Qm perceived to human vision is given by the weighted sum of each fundamental uj and the entry Cm(λj) corresponding to wavelength λj of the input block dye spectrum Cm.

Fig. 5 illustrates an example of how our vision system responds to a block dye spectrum with the reflectance 1.0 in the range of 470–510 nm. The profiles of 9 row vectors in the Matrix-R are shown sampled by Δλ = 5 nm step. According to the Eq. (8), the block dye input works to pass the the fundamentals {uj} in w = 470–510 nm just as a gate pulse. As a result, the integrated single spectral fundamentals passing through the block dye gate cause a dull fundamental Qm (red marked) perceived as a visible sensation. This is the first mathematical interpretation clarified in this paper, and it is due to the utility of the Matrix-R theory. Figure 6 illustrates the typical samples how the human vision perceives these optimal colors in relation to the block dye spectra.

Figure 6.

Visual response and color appearance for typical optimal colors.

Cm versus the fundamentals Qm as their visual responses. It should be noted that human vision cannot respond to sharp spectral changes in block dyes, and exhibits a dull responses.

Extraction of Optimal Colors by GBD Method

The generated block dye spectra are mapped to CIELAB color space. Figure 7 shows the color distribution for convex, concave and both block-dye chips in (a) N = 5112 (Δλ = 5 nm) and (b) N = 123552 (Δλ = 1 nm). Though the shell-shaped distributions are little bit sparse around the center, the outer surfaces both in (a) and (b) form the 3D gamut approximately close to the high precision model by Perales et al. [5] with Δλ = 0.1 nm. In practice, the color distributions in case (b) may be enough to get the optimal color gamut even if using such a rough sampling pitch as Δλ = 5 nm.

Figure 7.

Generated Block dye color chips with different resolutions in Δλ.

In this paper, the optimal colors are extracted by applying our GBD method [10] for the color distributions in Fig. 7. The GBD is represented by a set of maximum radial vectors {rGBD(θp, φq)} in the segmented polar coordinate as shown in Figure 8. The optimal colors are extracted as the surface colors located at the tips of the maximum radial vectors.

Figure 8.

GBD as a set of maximum radial vectors in Polar coordinates.

Letting the CIELAB value be QmLAB = [Lm∗, am∗, bm∗] for the fundamental Qm, the radial vector rm pointed to (θm, φm) from the centroid ropt is described as follows.

(11)

\begin{matrix} r_{m} (θ_{m}, φ_{m}) = Q_{m}^{LAB} - r_{0}; r_{0} = [L_{0}, a_{0}, b_{0}] = [{\bar{L}}_{m}^{*}, {\bar{a}}_{m}^{*}, {\bar{b}}_{m}^{*}] \end{matrix}

(12)

\begin{matrix} θ_{m} = {tan}^{- 1} (\frac{b_{m}^{*} - b_{0}}{a_{m}^{*} - a_{0}}); 0 \leq θ_{m} \leq 2 π \\ φ_{m} = \frac{π}{2} + {tan}^{- 1} (\frac{L_{m}^{*} - L_{0}^{*}}{{{(a_{m}^{*} - a_{0}^{*})}^{2} + {(b_{m}^{*} - b_{0}^{*})}^{2}}^{1 ∕ 2}}); \\ 0 \leq φ_{m} \leq π \end{matrix}

where, φm is treated as a positive value by adding the offset by π∕2.

Now, segmenting the radial vectors {rm(θm, φm)} to the fan-shaped sectors divided by (Δθ, Δφ) and finding the maximum vector in each sector, we get the GBD as a set of maximum radial vectors as shown in Eq. (13).

(13)

\begin{matrix} r_{GBD}^{opt} (θ_{p}, φ_{q}) = {max}_{m = 1}^{N} {r_{m} (θ_{m}, φ_{m})}; \\ 1 \leq p \leq P a n d 1 \leq q \leq Q \\ w h e r e, (p - 1) Δ θ \leq θ_{p} \leq p Δ θ \\ a n d (q - 1) Δ φ \leq φ_{q} \leq q Δ φ \\ Δ θ = 2 π ∕ P a n d Δ φ = π ∕ Q . \end{matrix}

Figure 9 shows a 3-D color solid constructed from the optimal colors extracted from the color distributions in Fig. 7. Here the color solid is rendered with GBD by the maximum radial vectors. The smoothness of gamut surface depends on the resolution Δλ and segmentation pitches (Δθ, Δφ) for the radial vectors {rm(θm, φm)}.

Figure 9.

Extracted optimal colors and formation of 3-D gamut.

Since the maximum radial vectors {rGBDopt(θp, φq)} are quantized to P × Q(p = 1 ∼ P, q = 1 ∼ Q), the number of optimal colors located at the tips of them is limited to at most M = P × Q. Though, all the fan-shaped sectors don’t always include the color chips but some of them become empty, because the color distributions of block-dye chips are not uniform in CIELAB space.

Indeed, in case of Fig. 9(a), P × Q = 16 × 16 = 256 optimal colors are expected to be found, but M = 241 colors are extracted with 15 empty sectors. Of course, even in this coarse resolution of Δλ = 5 nm, the number of extracted optimal colors could be increased to M = 677 by sub-dividing the sectors to P × Q = 32 × 32 = 1024, but the ratio of empty sectors relatively increases too.

In case of Fig. 9(b) with fine resolution of Δλ = 1 nm and P × Q = 64 × 64 = 4096, we could find M = 3565 optimal colors and create the smoother gamut, and moreover up to M = 12011 for P × Q = 128 × 128 with Δλ = 1 nm as shown in Table I below.

Table I.

Numbers of extracted optimal colors.

						Number of
Sectors		P × Q				Block dye

Resolution		16 × 16	32 × 32	64 × 64	128 × 128	Chips N
M	Δλ = 5 nm	241	677	1480	—	5132
M	Δλ = 1 nm	251	967	3565	12011	125332

Table I lists up the numbers of extracted optical colors.

Figure 10 shows a comparison with the standard sRGB and a wide gamut PDP display (Panasonic). Clearly the optimal color gamut is large enough to completely cover the actual device gamuts.

Figure 10.

Comparison in color gamuts between devices and optimal color.

Application to Image Gamut Expansion

The optimal color gamut is an ideal target for the imaging colorants or display devices. Although a variety of Gamut Mapping Algorithms (GMAs) [10] have been developed, most of them have aimed at compression from wide image gamut to narrow device gamut so far. As the imaging devices with wider color gamut developed, the expansion GMA for the images with narrower gamut than display or printer is required to reproduce the vivid and emotional colors. Our previous works proposed the Image-to-Device GMA [11] and compact description [12] of GBD by radial vectors and advanced to the image gamut expansion GMA [13].

Lastly, an application to the GBD-based image gamut expansion is challenged targeted on the optimal color gamut. Here the following two methods for image gamut expansion were comparatively tested.

5.1

Simple Expansion

A conventional simple method for image gamut expansion is to stretch the image CIELAB vector labimgorg by a gain factor G into the outer direction, getting the expanded result as

(14)

l a b_{img}^{expand} = G l a b_{img}^{org} .

5.2

Centroid-Invariant Adaptive Expansion (Proposed)

In contrast, the new method proposed in this paper expands a image CIELAB vector labimgorg so that the position of centroid immovable even after expansion like as

(15)

\begin{matrix} l a b_{img}^{expand} = G l a b_{img}^{org} + (1 - G) r_{img} \\ w h e r e, r_{img} = C e n t r o i d [l a b_{img}^{org}] . \end{matrix}

Here, rimg means the centroid of original image color distribution.

As a measure, the gain factor G > 1 may be decided statistically, with reference to the standard deviation ratio of optimal color versus original image color GBDs as

(16)

\begin{matrix} G = G_{0} (σ_{opt} ∕ σ_{img}) \\ σ_{opt} ∕ σ_{img} = S_{igma} [{r_{GBD}^{opt} (θ_{p}, φ_{q})}] ∕ S_{igma} [{r_{GBD}^{img} (θ_{p}, φ_{q})}] . \end{matrix}

The constant G0 is adjusted not to exceed the optimal color gamut boundary considering the image color GBD

r_{GBD}^{img} (θ_{p}, φ_{q})

Figures 11–13 show the gamut expanded examples for typical three images with high, medium, and low saturations.

Figure 11.

Image color gamut expansion example (amateur Photo).

Figure 12.

Image color gamut expansion texample (standard image).

Figure 13.

Image color gamut expansion example (low saturation image).

Fig. 11 is an amateur photo with good color reproduction. Although it seems unnecessary to expand the color gamut, there is still a small amount of space that can be stretched compared to the optimal color gamut. In the simple expansion result (b), the colors are overflowing a bit beyond the boundary for the gain factor G = 1.3, while they are just fitted inside the optimal gamut shell for the same gain factor G in the result (c) by the proposed method . The colors in blue sky or red roof of tower are well expanded and nicely reproduced in vivid and are clean.

Fig. 12 is a result for “Harbor” with medium saturation. This is a kind of standard image but it looks a little desaturated. In Fig. 11, the image gamut was sucessfuly expanded to be just fitted inside the optimal color gamut for the gain factor G = 1.34 by the proposed method as shown in (c), while the simple expansion result (b) is causing a little overflow for the same gain factor G, because the gravity center of expanded color distribution moved upwards.

Fig. 13 is an example which still has room in the color space for gamut expansion. In this sample, it was possible to expand up to G = 1.65, which is the very limit of the optimal color gamut boundary by the adaptive method as shown in (c), while the colors much overflowed after the simple expnsion in (b).

Additional Expansion Tests & Discussion

Figures 14–16 show additional test resultes for different type of images from Figs. 11–13.

Figure 14.

Image color gamut expansion texample (standard Movie).

Figure 15.

Image color gamut expansion texample (standard Movie).

Figure 16.

Image color gamut expansion texample (amateur Photo).

Fig. 14 is the expanded result in JPEG still image picked up from the test movie named “Euro Market” with high saturation.

Although this image seems unnecessary to expand the color gamut similar to Fig. 11, There is still some room for expansion, and surprisingly, it could be expanded with gain G = 1.3. of course using the proposed Centroid-invariant method [B].

Fig. 15 is another sample applied to the well known test movie “Street Car”. Since this image is less saturated as compared with “Euro Market”, it could be expanded up to the very edge of the gamut boundary of the optimul colors with G = 1.52.

Fig. 16 is a professional photo taken under clear blue sky. In this sample, the gain factor G was automatically set to G = 0.975 according to Eq. (16). It showed the lowest value among all tested images. If G = 1, no color gamut expansion is performed as indicated by Eq. (15), so the gamut expansion rate in this example was also the lowest value 0.85 as shown in Table III.

In any of all above examples, the reason why the proposed expasion method [B] is significantly better than simple expansion method [A] is that the center of gravity of the color distribution after expansion is unchanged while maintaining the center of gravity of the original image color distribution.

The proposed Centroid-invariant Adaptive Expansion [B] is fundamentally different in principle from the conventional methods, and is realized by the simple but clever formula Eq. (15).

The feature is that the expansion is performed by averaging the color vector labimgorg of each pixel and the centroid rimg of the original image with weights G and (1-G).

Measuring Expansion Rate of Gamut Volume

The Gamut expansion effect can be measured by the increase in gamut volume. Since the calculation of 3-D gamut volume for complicated color disribution is not easy, here we roughly estimated it by an ellipsoidal approximation.

The 3D shape of clustered color distributions as shown in Figs. 11–13 is fitted to an ellipsoid whose semi-axes are estimated using PCA (Principal Component Analysis), then the geometric volume of ellipsoid is mathematically given by

(17)

V ol {ellipsoid} = (4 π ∕ 3) \sqrt{λ_{1}} \sqrt{λ_{2}} \sqrt{λ_{3}},

where, {λ1, λ2, λ3} denotes 1st, 2nd and 3rd eigenvalues.

Here, their square roots correspond to the half axes of ellipsoid.

Thus each gamut expansion rate for the images of Figs. 11–13 was measured by the rate of gamut volume after versus before expansion Vol{expanded} versus Vol{original} noted as

(18)

V ol Gain = V G = V ol {expanded} ∕ V ol {original} .

Table II summarizes the gamut expansion rate for each image.

Table II.

Gamut expansion rate.

Image	Lake	Harbor	Sagano
V G	0.987	1.765	3.105

As well, the gamut expansion rate for the additional images of Figs. 14–16 was measured as shown in Table III.

Table III.

Gamut expansion rate (additions).

Image	Euro Market	Street Car	Mt. Fuji
V G	1.271	1.280	0.850

Discussions

The results in Table II show that the Lake image does not have an expansion effect and retains its original volume. This seems strange at first glance, but the reason is that this source image is originally highly saturated and there is almost no gap to the color gamut boundary, and it tells us that expansion beyond 1 is impossible, so it is a convincing result.

In addition, for low-saturation images such as Harbor and Sagano, the expansion rate seems to be automatically adjusted adaptively to the saturation of the image. It can be said that the proposed model worked reasonably.

Table III, on the other hand, tells an interesting result. Among all the images tested in this paper, image 16 showed the lowest values for both G and expansion rate VG. Only the G value is less than 1.0, which means that it is the most difficult to expand the color gamut. This image is believed to have been taken by a professional photographer. Could it be an indicator of skill? Very interesting.

The constant G0 is set to around 0.5 in all of the above samples. Though it should be optimized in more rational and theoretically considering the relation between the both GBDs of given image and the optimal colors characteristics. Development of more rigorous mathematical optimization method for the gain factor G adaptive to any image is left behind as a future work.

Conclusions

This paper discussed on the optimal colors afresh from a different point of view. A harvest is summarized as follows.

(1)

A simple and easy method for shaping the optimal color gamut by GBD is proposed.

(2)

Visual spectral response to block dye is analyzed for the first time based on the Matrix-R theory and clarified how their dull responses appear as a result of integrated fundamentals to the monochromatic single spectal stimuli.

(3)

A novel Centroid-invariant image gamut expansion method is first introduced. Optimal color gamut is utilized as an ideal target and succeeded in improving the color appearances of low-saturation images by expanding their color gamuts maintening the gravity center of color distribution in original image.

References

1SchrodingerE.1920The theory on pigments of high luminosityAnn. Phys.4603622603–2210.1002/andp.19203671504

2OhtaN.Introduction to Color Reproduction Technology1997Corona Publishing Co., Ltd.Tokyo, Japan107

3MacAdamD. L.1935The theory of the maximum visual efficiency of colored materialsJ. Opt. Soc. Am.25249252249–5210.1364/JOSA.25.000249

4WestG.BrillM. H.1983Conditions under which Schrödinger object colors are optimalJ. Opt. Soc. Am.73122312251223–510.1364/JOSA.73.001223

5PeralesE.EstevanT. M.PérezV. V.de FezD.PérezE. G.Martínez-VerdúF. M.2005A new algorithm for calculating the MacAdam limits for any luminance factor, hue angle and illuminantProc. AIC Colour05737740737–40

6JiangF.FairchildM. D.MasaokaK.2020Effect of peak luminance on perceptual color gamutProc. IS&T CIC28: Twenty-eighth Color and Imaging Conf.131813–8IS&TSpringfield, VA10.2352/issn.2169-2629.2020.28.3

7ContoreP.2013A zonohedral approach to optimal coloursCol. Res. Appl.38110119110–910.1002/col.20713

8CohenJ. B.1988Color and color mixtureCol. Res. Appl.135395–3910.1002/col.5080130106

9CohenJ. B.Visual Color and Color Mixture: The Fundamental Color Space2001Illinois PressUrbana, IL

10MorovicJ.LuoM. R.2001Evaluating gamut mapping algorithms for universal applicabilityCol. Res. Appl.268510285–10210.1002/1520-6378(200102)26:1<85::AID-COL9>3.0.CO;2-2

11ChenH. S.KoteraH.1999Adaptive gamut mapping method based on image-to-deviceProc. IS&T NIP15: Fifteenth Int’l. Conf. on Digital Printing Technologies346349346–9IS&TSpringfield, VA10.2352/ISSN.2169-4451.1999.15.1.art00090_1

12KoteraH.SaitoR.2003Compact description of 3D image Gamut by r-image methodJ. Elect. Imag.12660668660–810.1117/1.1605418

13SaitoR.KoteraH.2004Image-dependent three-dimensional gamut mapping using gamut boundary descriptorJ. Elect. Imag.13630638630–810.1117/1.1758727

14ChenH. S.KoteraH.2002Three-dimensional gamut mapping method based on the concept of image-dependenceJ. Imag. Sci. Technol.46446344–6310.2352/J.ImagingSci.Technol.2002.46.1.art00007

15KoteraH.MitaT.Hung-ShingC.SaitoR.Image-dependent gamut compression and extensionProc. IS&T PICS Conf.2001IS&TSpringfield, VA288291288–91

16KoteraH.SaitoR.Color Image Processing, Chap. 32007CRC PressBoca Raton, FL