1.
Introduction
Colored filters have been historically used in photography to modulate the color of the prevailing illuminant. A filter is usually a piece of colored glass (or another substrate) that is placed in front of the lens of the camera leading to a change in the colors of the scene in the acquired photo. One of the main goals of using these filters is to change the way the camera sees the light, which depends on the spectral properties of the filter used. As an example, a ‘warm’ filter can be used when taking a picture under a cool light in order to render the effective illuminant color neutral.
A black-body radiation can be modeled by Planck’s law or Wien’s approximation of this law [
1]. A Planckian light, by definition, is dependent on a single number, the color temperature (measured in Kelvin). As we move from 3000 to 5000 to 10,000 Kelvin the corresponding Planckian light ‘looks’ yellowish, whitish, and bluish respectively. The higher the temperature the cooler the color of the light. The Planckian locus is the line that connects the chromaticity points of the series of color temperatures of black body radiators. The Planckian locus is plotted with respect to the
uv chromaticity diagram in Figure
1 (blue solid line). From right to left, the color temperature varies from 4000 to 20,000 K.
In daily life, most lights have spectra that are not well described by the Planckian or Wien-Planckian equations (mostly, we will consider the Wien-Planckian lights in this paper). These include natural light sources such as the sun and sky, and artificial ones like incandescent lamps and LED lamps. However, these non-Planckian illuminants can, in analogy to the temperature defining Planckian lights, be characterized by their correlated color temperatures (CCT). The CCT is the temperature of the Planckian illuminant having the closest chromaticity coordinates to those of a given illuminant [
2].
Regarding daylights, there is a second
daylight locus (also plotted on the chromaticity diagram for the 4000 to 20,000 K CCT range, the red dash-dotted line in Fig.
1) that accounts for the colors of some daylights. Given a target CCT, the corresponding chromaticity point on the daylight locus can be found and the corresponding daylight spectrum [
3] can be calculated. In the standard daylight nomenclature, D100 and D40 correspond to 10,000 K and 4000 K CCT daylights.
Figure 1.
(a) Planckian locus (blue solid) and daylight locus (red dash-dotted) in u,v chromaticity diagram. (b) Zoomed in.
![]()
In this study, we investigate how colored filters filter illuminants. Prior research in the literature that has considered this question has focused on finding a particular filter that changes a specific illuminant in the scene to another chosen one. Gage [
4] presented a study of the properties of a filter that brings a Wien-Planckian illuminant with one color temperature to another specific one. It also turns out that a Gage-filter maps any Wien-Planckian to another Wien-Planckian (our own analysis starts with this result). For known film-types, given lights, and a set of approximate, physically realizable, Gage-type filters, McCamy [
5] investigated how these filters could be practically used to optimize the exposure of color films. Importantly, it was observed by Henry Hemmendinger— and reported in [
6]—that the yellowing of the lens of the eye as we age can be thought of as approximately following a Gage-type equation. In related research, Weaver [
7] and Estey [
8] respectively considered the filter design question from a theoretical (what filters we might design) and practical (how do commercial filters filter light) viewpoints.
Interestingly, the question of how filters modulate arbitrary light had not, to our knowledge, been considered quantitatively till our previous work [
9] on locus filters. There, we showed that it was possible to design a filter that guarantees that the resulting light stays on the Wien Planckian locus. We called such a filter a ‘Locus Filter’ and presented a physical basis for the design of such filters. A locus filter maps a given input color temperature to an output temperature. The mapping function, which we discuss in the next section, is non-linear. Significantly, it was proven [
9] that the locus filters are the only ones that have the property that they map Wien-Planckian lights to other lights that are also Wien-Planckians.
We investigate further the behavior of locus filters in general and how they filter daylights in particular. Using standard daylights as a useful single parameter family of lights (i.e., they are parameterized by their correlated color temperature (CCT)), we can place Wien-Planckians in correspondence with daylights. Each pair has a Wien-Planckian with a given color temperature and a daylight with the same CCT. Then, we asked the following question: does there exist a correction filter that takes each Wien-Planckian to its corresponding daylight? We find, to a good approximation, that such a filter exists. We also show that when daylights and Wien-Planckians are in this ‘filter’ correspondence, a locus filter (designed for Wien-Planckians) must map a daylight with a given CCT to another daylight. Moreover, the CCTs for daylights shift in the same way as the corresponding Wien-Planckians.
Our new correction filtered representation of daylights results in a new daylight locus which is found to be very similar to the current locus. Usefully, our new daylight equation is similar in structure to the Wien-Planckian equation and, daylight spectra are simple (and intuitive) to generate. In contrast, the existing standard daylight methodology [
3] is a little cumbersome to implement. Additionally, being able to obtain daylights by applying a filter to Wien-Planckian lights has direct application in computer vision. The Wien approximation of Planck’s law has the nice property that the logarithm of spectral band-ratios (e.g., r/g and b/g) of Wien-Planck lights fall along a line. This linear constraint has proven to be very useful in calculating light-intensity independent invariants which in turn has made it easier to detect and remove shadows from images and to solve for color constancy e.g., see [
10–
12]. The work in this paper, in effect, extends this prior art in computer vision to also be applicable for daylights that lie on or close to the daylight locus.
In a second contribution of this paper, we wished to compare locus filters to already existing Kodak Wratten filters that are, analogously, designed to change the color temperature of lights. We will examine the color filtering performance (effectively, how much like locus filters they are) for four Kodak Wratten filters [
13].
The rest of the paper is organized as follows. In Section
2, we present the physical and mathematical basis for the design of locus filters. Then, in Section
3, we apply locus filter theory to daylights. We solve for a color filter that—to a good approximation—places Wien-Planckian lights with given temperatures in correspondence with daylights that have the same
CCTs, and we empirically demonstrate that locus-filtered daylights stay on the daylight locus, and they shift in color temperature as if they were Wien-Planckians. In Section
4, we study empirically how well our daylight filter model daylights, and how locus filters affect daylights. Additionally, we compare some commercially existing Kodak filters to locus ones in terms of the changes they exhibit on lights. The paper concludes with Section
5.
2.
The Locus Filter
In a Lambertian scene, sensors responses (of a camera or XYZ color matching functions (CMFs))
ρk can be written as a function of their spectral sensitivities
Qk(
λ) (where
k =
R,
G,
B for RGB camera sensors or
k =
X,
Y,
Z for color matching functions), the surface spectral reflectance
S(
λ), and the spectral power distribution of the illuminant
E(
λ):
where
ω is the range of visible wavelengths [
1].
Ignoring complexities such as interreflections, when a colored filter is put in front of the lens of the vision system, the filtered sensor responses
ρkF can be written as:
F(
λ) defines the filter spectral transmittance.
A Planckian black-body illuminant
EP is a function of color temperature
T and wavelength
λ, and is written as [
1]:
where
c1 and
c2 are constants equal to 3.74183 × 10
−16 Wm
2 and 1.4388 × 10
−2 mK, respectively. The scalar
k modulates the intensity of the Planckian light [
1].
In the range of typical lights (2000 K to 20,000 K), a simple approximate form of Planck’s equation—called Wien’s approximation [
14]—can be used to describe black body illumination. These Wien-Planckian lights are written as:
Here,
k modulates intensity and the constants
c1 and
c2 are as defined after Eq. (
3).
Based on the Wien approximation of Planck’s law, a locus filter can be designed [
9]. A locus filter takes a Wien-Planckian illuminant with a temperature
T1 to a second Wien-Planckian with a temperature
T2. By dividing the spectra of these two illuminants (Eq. (
4)), a filter transmittance function
FLocus(
λ,
Tf) is obtained:
The
Tf parameter is called
the locus filter temperature (LFT) [
9], and is equal to:
It is clear from Eq. (
6) that LFT,
Tf, is not uniquely defined by the pair of Wien-Planckian lights with temperatures
T1 and
T2. That is, there are many temperature pairs that can lead to the same LFT. Also following from Eq. (
6), the LFT can be negative.
Let us now calculate the product of the filter
FLocus(
λ,
Tf) with a third light that has a temperature
T3 to make a new light spectrum
Enew(
λ) [
9]:
Clearly,
Enew(
λ) lies on the Planckian locus with temperature
Tnew calculated as [
9]:
In summary, a locus filter is designed to map a light of one color temperature to another and is parameterized by its LFT. Equation (
7) asserts that a given locus filter will map any Wien-Planckian to another light that is also a Wien-Planckian and Eq. (
8) states the formula for calculating the temperature of filtered light (given knowledge of the temperature of the unfiltered light and the locus filter’s LFT). Taken together, these equations also teach that given a single Wien-Planckian with a temperature
T we can generate all Wien-Planckian lights (for any color temperature) given an infinite set of locus filters with the requisite LFTs.
Importantly, it has been proved [
9] that the form of the filter equation is unique. That is, there is no other filter which always maps all Wien-Planckian lights to corresponding lights that themselves are Wien-Planckians.
We note that the definition of locus filter has another degree of freedom. Specifically, we can scale the locus filter to transmit more or less light. In Eq. (
9), we add the scalar
μ to model this variable transmittance. Clearly, if one locus filter is a scalar, say <1, from another then it will map Wien-Planckian lights to the same counterparts but they will be darker [
9].
The change of temperature after applying the filter depends on both the initial temperature of the Wien-Planckian light and the LFT of the applied filter (see Eq. (
8)). In order to observe the nature of this change, we apply some locus filters with different LFTs with positive and negative values to several Wien-Planckian lights with different color temperatures. The first three columns of Table
I shows the change of temperature when applying locus filters with a positive LFT of 5000, 7500 and 10,000 to different Wien-Planckian illuminants. The last two columns of Table
I are for the negative LFTs, −12,000 and −20,000. Note from Table
I that filtering a Wien-Planckian light with a filter with positive LFT always makes the light warmer and conversely, a negative LFT will result in a filter that will always make lights cooler in appearance.
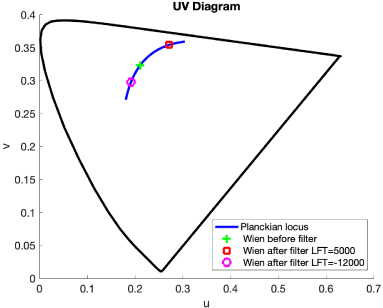
In Figure
2, we show in the
u,
v chromaticity diagram, how a Wien-Planckian light with a color temperature of 5000 K shifts differently when being filtered with two different locus filters. In the first case, the light is filtered with a locus filter with a positive temperature (LFT = 5000) making it warmer. In the second case, the same light is filtered with a locus filter with a negative temperature (LFT = −12,000) which makes it cooler. In both cases, the new lights are, as they must be, on the Wien-Planckian locus.
Curiously, Eq. (
8) also indicates that a filtered light can have a negative color temperature but, of course, this is not physically possible. However, for the purposes of our work we will allow negative color temperatures (see [
9] for more details). A negative color temperature Wien-Planckian results in all positive light spectrum but that it is even bluer than an infinite color temperature light. In Figure
3, we show on the uv chromaticity diagram the Planckian locus in solid blue and the additional colors in an extended locus are shown in a red dotted line. This extended locus allowed the negative color temperatures. To elaborate this point on the Planckian locus from left to right the temperature monotonically decreases from lim
T→∞ to lim
T→0+. Conversely, in the extended locus from right to left the temperature monotonically increases from lim
T→−∞ to lim
T→0− [
9].
Figure 2.
Color temperature shifts on the Planckian Locus in the u, v chromaticity diagram after applying two different locus filters, one with a positive LFT and the other with a negative one.
![]()
Figure 3.
The Planckian locus and the extended locus.
![]()
Table I.
Colour temperature shifts after applying locus filters on Wien-Planckian lights. Column one records the colour temperature in Kelvin for 4 input lights, ranging from 4000 to 10,000 K. The columns show the LFT ranging from −20,000 to 10,000 K. In position (i, j) we see the output colour temperature for the ith input light filtered by a locus filter with the jth LFT.
| Input light temperature | Output colour temperature for LFT (Tf) |
|---|
| (5000) | (7500) | (10,000) | (−12,000) | (−20,000) |
|---|
| 4000 K | 2222 K | 2609 K | 2857 K | 6000 K | 5000 K |
| 6000 K | 2727 K | 3333 K | 3750 K | 12,000 K | 8571 K |
| 8000 K | 3077 K | 3871 K | 4444 K | 24,000 K | 13,333 K |
| 10,000 K | 3333 K | 4286 K | 5000 K | 60,000 K | 20,000 K |
3.
From Wien-Planckians to Daylights
We see in Fig.
1, a pictorial representation of the daylight locus in the
uv chromaticity diagram. Visually, the daylight locus runs parallel to the Planckian locus. Ultimately, in this section we propose a simple and
elegant formula for generating a daylight spectrum, given a target CCT. We claim elegance as—we shall see—our formula is simple (as simple as the Wien approximation formula itself) and, because—in comparison to our new formula—calculating daylight spectra using the conventional methodology [
3] is slightly laborious. We recapitulate the standard daylight calculation below.
Given a desired correlated color temperature (CCT)
T we, first, calculate the
xT chromaticity coordinate [
1] of the light with this temperature according to:
Now, the
yT chromaticity coordinate [
1] is calculated:
The daylight spectrum
ET(
λ) which corresponds to (
xT,
yT) is formed as a weighted sum of
E0(
λ),
E1(
λ) and
E2(
λ) (the spectra are principal component lights that result from an analysis of Judd [
15]) as follows:
where
m1 and
m2 are defined as [
1]:
In this paper, we replace the standard daylight spectral calculation with the simple formula:
where
C(
λ) denotes a fixed filter
correction function and the superscript
C indicates that we are using the correction filter form of the daylight calculation (and not the standard methodology). The meaning of
T here is correlated color temperature (or equally temperature as it applies to the Wien equation). The other terms are as before (see Eq. (
4)). Equation (
15) asserts that Wien-Planckians and daylights with the same temperature are in one-to-one correspondence where one is mapped to the other by
C(
λ). See Figure
4 for the
C(
λ) that is empirically derived.
With this derivation, it is possible to find a correction filter that—more or less—maps Wien-Planckians to daylights. The details of how we solve for the filter are presented, next, in Section
3.1.
3.1
Solving for the Correction Filter
In order to obtain the correction filter
C(
λ), let us represent spectra as vectors. For a given temperature
T and a Wien-Planckian
E(
λ,
T) we denote the corresponding light vector as
. If the visible spectrum is represented at 10 nanometers sampling from 400 nm to 700 nm, then
is a 31-component vector. According to Eqs. (
10)—(
14) for a CCT of
T we can calculate a corresponding daylight spectrum which we denote as an n-vector
(where n is typically 31). Also, representing the function
C(
λ) as the n-vector
, we rewrite Eq. (
15) in the discrete domain:
where diag() takes a
n-vector and places its components along an
n ×
n diagonal matrix.
Supposing that we have a set of the spectra of
N daylights,
, having (correlated color) temperatures, [
T1,
T2, …,
TN], respectively. For the same temperatures, we calculate Wien-Planckian lights
(where the scaling term in Eq. (
4) is assumed to be equal to 1). For this set of corresponding (matched temperature to correlated color temperature) Wien-Planckians to daylights we, simplistically, might think of finding a filter such that:
However, by the different natures of the equations that define Wien-Planckians and daylights, we admit a per temperature scaling factor
k that can be applied. Let us denote the
N scaling factors as the vector
k. The approximation is now written as:
We observe that Eq. (
16) can be written as:
where the symbol ⊙ denotes the component-wise multiplication of two matrices and
t—here and henceforth—denotes a matrix/vector transpose.
Considering the individual components, we would like:
where
i∈[1,2, …,
n] and
j∈[1,2, …,
N]. Expressing this approximation in log units, we use the superscript
′ to denote log-values. Then, recalling that multiplication becomes addition in log space, we can write:
Rewriting Eq. (
21) in matrix form:
where each component of the respective
N and
n dimensional vectors
and
is equal to 1. Now, let
Ci denote a
n ×
N matrix that has 1s in the
ith row but is zero, everywhere else. Similarly, let
Kj denote a
n ×
N matrix that has 1s in the
jth columns but is zero everywhere else. Then:
and:
Equivalently, we can write Eqs. (
23) and (
24) as:
and:
Here vec() is the operator that turns matrices into vectors (where columns are stacked on top of each other). Respectively, the ith and jth columns of the nN × n and nN × N matrices MC and MK are vec(Ci) and vec(Kj).
We are now in a position to write an optimization statement that we would like to minimise:
where ∥. ∥
F denotes the Frobenius norm [
16]. Substituting (
Ψ′−
Ω′) with
B:
Now we use the vec() function again and write:
Notice that the vec operator does not change the meaning of the equation. Rather, tables are transcribed to vectors but the same components are in correspondence. Substituting Eqs. (
23) to (
26) into (
29):
Denoting
we would, equivalently, like to find
and
k′ that minimizes
Let us define the
nN × (
n +
N) matrix
A = [
MCMK] and the
n +
N coefficient vector
(where “;” means stacking the vectors on top of each other). Effectively, we have written our minimisation in the form
which can be solved in closed form using the Moore-Penrose inverse (
) [
17]. The solution
simultaneously solves for the filter and the scaling components. Since this minimisation is carried out in log space, the final correction filter
is equal to
.
The reader will note that we have carried out the minimization in log units. Of course, we did this to arrive at a closed-form solution. To our knowledge, there does not exist a closed form solution to Eq. (
19).
Root Mean Squared Log Error minimization is commonly used and, in effect, minimizes relative error, e.g. [
18].
3.2
Applying a Locus Filter to Daylight Illumination
Returning to Eq. (
15) a daylight spectrum
DC(
λ,
T),
corrected from a Wien-Planckian light with the same temperature
T can be written as:
This is opposed to (no superscript) the standard daylight calculated according to Eq. (
10)—(
14), denoted
D(
λ,
T).
Now, suppose we have a locus filter
FLocus(
λ,
Tf) such that a Wien-Planckian with temperature
T1 is mapped to
T2:
Applying the same locus filter to a daylight with a correlated color temperature
T1 gives:
Substituting Eq. (
33) into Eq. (
34) gives:
and from Eq. (
32) it follows that:
Therefore, we can conclude that when a locus filter is applied to a daylight it will introduce the same shift in correlated color temperature as if it was applied on a Wien-Planckian illuminant with the same temperature.
4.
Experiments
4.1
Finding the Correction Filter
To find the daylight filter
C(
λ) that brings any Wien-Planckian light to a daylight with the same color temperature, we start with a set of 21 Wien-Planckian lights that are equally distanced in terms of their mired color temperatures. The mired color temperature [
19] (micro-reciprocal-degree), is often used to measure how similar one light color is to another. It is measured in mired units and can be calculated from a color temperature
T as follows:
For our set of 21 Wien-Planckian lights, the mired color temperatures range from 50 to 250 with 10 mired step corresponding to color temperatures from 4000 K to 20,000 K with a non-uniform step. For each of these lights, we obtain an equivalent standard daylight with the same correlated color temperature (see start of Section
3 for equations on how this is done). Given these two sets of lights—Wien Planckians and standard daylights—we find a correction filter
C(
λ) as set out in Section
3.1. The correction filter—which, we interpret here as a transmittance filter—is shown in Fig.
4.
Figure 4.
Transmission spectrum of the correction filter.
![]()
In order to validate the accuracy of the performed optimization, we calculate the difference between each original daylight and its reconstructed counterpart given the correction filter
C(
λ). For convenience, we represent the spectral functions of these two lights as vectors of measurements at a discrete number of sample points across the visible spectrum, which we denote
and
(for respectively the standard and corrected form of our daylights). Here we sample spectra at 10 nanometre samples from 400 to 700 nanometers (for the visible spectrum). We are most interested in how similar the shape of these daylights spectra are to one another. So, we use the angular error as an error metric:
where “.” denotes the vector dot-product, ∥. ∥ is the vector magnitude and acos is the inverse cosine. We also calculate a percentage root mean square error measure. As there is a brightness difference between the spectra we normalise the actual daylight and the one predicted using the correction filter approach by their norm (respectively
and
). We calculate the magnitude of the vector distance between these normalised vectors. As the vectors being compared have unit length they can be visualise as vectors whose tips lie on a unit (hyper sphere). In this visualization the largest distance between the tips of any two vectors has to be 2. Thus, we divide by 2 to return a percentage error.
where ∥. ∥ is the L2-norm.
We found that the average angular error between the ground-truth daylights and the reconstructed ones using the daylight filter for the 21 lights used in the optimization is , and this corresponds to a 1%RMS. The maximum angular error was just (2%RMS). These values indicate that the daylight filter gives very close spectra to the original daylights.
In Figure
5, we show two examples of spectral power distributions of original daylights and their reconstructed ones using the daylight filter. The first example corresponds to the case where the error between the two lights is equal to the mean error found after the optimization (
angular error or 1%RMS). The second example corresponds to the maximum error found after optimization (
angular error or 2%RMS). One can observe that in the case of maximum error the two spectra are still quite similar.
Figure 5.
Comparison of spectral power distributions of an original daylight and a reconstructed one using the daylight filter; (a) The error between the two spectra is equal to the average value (1.1 angular error or 1%RMS) found after optimization. (b) The error between the two spectra is equal to the maximum value (2.3 angular error or 2%RMS) found after optimization.
![]()
4.2
Extending the Daylight Locus
The method for calculating standard daylights was not designed to be used for creating daylights with a correlated color temperature less than 4000 K. Although lower values CCTs are possible at sunrise and sunset (and are found in measured daylights [
20]). Creating daylights for correlated color temperatures lower than 4000 K is made possible with our method. For any CCT, we simply calculate our daylight spectrum using Eq. (
15).
In the Granada set of daylights [
20] there is a daylight spectrum that has a CCT of 3888 K (with respect to which we cannot calculate a standard daylight spectrum). In Figure
6 we plot the spectral power distribution of this measured daylight and the SPD calculated with our correction filter using Eq. (
15) (both lights are normalized so their maximum relative power is equal to 1). The angular error and %RMS between these two SPDs are equal to 7.5
and 6.5%, respectively.
Figure 6.
Comparison of spectral power distribution between a measured daylight in Granada set whose CCT is equal to 3888 and its reconstructed counterpart (with the same CCT) using our daylight filter.
![]()
Additionally, using our new formula for daylights (Eq. (
15)), we can calculate the chromaticities for a range of CCTs and make a new daylight locus. In Figure
7, we plot, in the
u,
v chromaticity space, both the standard daylight locus and our new correction-filter-based locus. Notice how similar the two loci are to one another (unsurprising given the closeness of the spectral fits). As our approach allows us to obtain daylights for color temperatures less than 4000 K, the dotted line in Fig.
7 shows the extended daylight locus for color temperatures between 2000 K and 4000 K (for which the conventional daylight locus is not defined).
Figure 7.
Ground truth daylight locus (blue solid line) and our reconstructed (red, dashed) plotted in the u, v chromaticity diagram. The dotted red line shows the extension of the daylight locus for color temperatures less than 4000 K.
![]()
4.3
Locus Filter Applied to Daylights
We have shown in our previous work [
9] that the shift of CCT introduced by a locus filter when applied to real lights follows very closely the shift seen by an equivalent Wien-Planckian illuminant (by equivalent we mean its color temperature is equal to the correlated color temperature of the real light) after applying the same locus filter. In the Section
3.2, we have, in effect, shown that we expect the shift in CCTs of daylights to follow the temperature shift in the corresponding Wien-Planckians when a locus filter is applied.
Let us now consider how the CCTs for the 99 (complete set of) measured daylights in Granada [
20]—which do not lie on the daylight locus—shift when they are filtered by a locus filter. First, let us measure how far these lights are from the daylight locus built using our new daylight Eq. (
15). For the
ith daylight,
DiG(
λ) in the Granada set (superscript
G for
Granada), we obtain its CCT,
Ti, using the method [
21]. We calculate the 99 CCTs: {
T1,
T2, …,
T99} for the 99 Granada daylights. Eq. (
4) is then used to obtain a Wien-Planckian light
Ei(
λ,
Ti) (where we interpret the CCT for the
ith Granada daylight as a temperature for the Wien-Planckian equation). Applying our correction filter
C(
λ) to this light will give a daylight with the same CCT:
DC(
λ,
Ti).
Let us denote the
u′v′ 2-component vectors for the Granada daylight and its closest locus counterpart as
and
respectively. The average, median, maximum and 95th percentile of
Δu′v′ over the 99 Granada daylights are reported in the first column of Table
II. The just noticeable difference (JND) of this chromaticity distance has been found to be 0.004 [
22,
23]. So, on average, the Granada daylights are so close to their daylight counterparts that their differences in color are close to being imperceptible. Though, there are lights up to 5 JNDs from the daylight locus.
Now we consider how the Granada daylights change when they are filtered by a locus filter. Clearly, by construction, a daylight that is on the daylight locus will shift as predicted by Eqs. (
8) and (
35). That is, given the correlated color temperature of a locus daylight and the LFT of the filter we can predict, in closed form, the CCT of the filtered light. How do we quantify what happens when off-daylight-locus illuminants are filtered by a locus filter?
As remarked earlier (after Eq. (
8)) a single-color temperature and the set of locus filters generated by the set of all LFTs exactly generates all Wien-Planckian lights. The same is true for our corrected daylight formalism. A single daylight
DC(
λ,
T) is mapped to all other daylights through the appropriate choice of LFT and locus filter. That is every Wien-Planckian or every corrected daylight itself
seeds the whole (Planckian or daylight locus).
Similarly, an arbitrary daylight drawn from the Granada set will also induce its own locus of filtered lights (when all locus filters are applied). Intuitively, we would like these per Granada loci to be ‘like’ either the Planckian locus or, equivalently, the corrected daylight locus. Let us denote the chromaticity coordinates of the filtered Granada daylight and the corrected daylight (with the same CCTs) respectively as and (where f denotes dependence on a locus filter).
We can calculate
and
. By our intuition of parallel locii, we’d like
Δi ≈
Δif. If this distance is constant for each LFT then each Granada light would induce a locus parallel to the Planckian or corrected daylight locus and the distribution of temperatures across the locus would be the same. We additionally report in Table
II the mean, median, max and 95th percentile of
Δif after applying locus filters with locus-filter-temperature of 5000, 8000, 12,000 and −12,000. We find that the average chromaticity distance for locus filtered daylights is broadly equal to the unfiltered case except for the case of a negative LFT. But it is still, on average, within the range of just noticeable distance (JND = 0.004).
Table II.
The mean, median, max and 95th percentile of chromaticity difference Δu′v′ between a locus filtered Granada daylight and a daylight filtered Wien-Planckian with a colour temperature obtained after applying the locus filter.
| LFT | Unfiltered | 5000 | 8000 | 12,000 | −12,000 |
|---|
| Mean Δu′v′ | 0.004 | 0.004 | 0.004 | 0.004 | 0.005 |
| Median Δu′v′ | 0.003 | 0.002 | 0.002 | 0.002 | 0.004 |
| Max Δu′v′ | 0.019 | 0.030 | 0.024 | 0.021 | 0.021 |
| 95th% Δu′v′ | 0.010 | 0.019 | 0.014 | 0.013 | 0.013 |
Figure
8 shows Granada daylights and filtered ones with two different locus filter temperatures in the
u,
v chromaticity diagram. As expected (predicted by the previous experiment), the Granada daylights shift along the locus. Left, a positive LFT shifts the
u,
v chromaticities for the Granada Daylights (blue stars) toward warmer colors (green circles). A negative LFT, see panel b, makes all the Granada daylights cooler (higher CCT).
Figure 8.
In u, v chromaticity coordinates we show the Planckian locus (black solid), our daylight locus (red dashed line) and its extension (red dotted line) to color temperatures less than 4000 K (red); (a) Granada lights and locus filtered ones with a locus filter temperature of 5000. (b) Granada lights and locus filtered ones with a locus filter temperature of −12,000.
![]()
4.4
Wratten Filters versus Locus Filters on Measured Lights
In this section, we will consider the extent to which some Wratten filters filter light like locus filters. There is a large number of Wratten filters—which filter light in a variety of ways—and they are used in photographic, scientific and technical research and applications. These filters are organized into categories depending on the effects they have on the acquired image, and they are characterized by a coding system where each filter is referred to by a unique code.
Here, we consider four of the Kodak Wratten filters from two different categories: the 81 and the 82 which belongs to the light balancing category, and the 80A and the 85 from the color conversion category. Light balancing filters cause minor adjustments in the color temperature of an illuminant giving a cooler (the case of 82) or a warmer (the case of 81) light. Whereas color correction ones enable significant adjustments in the color temperature of an illuminant leading to a cooler one (the case of 80A) or a warmer one (the case of 85).
We would like to consider the extent that these filters change lights like locus filters. To do so, we need first to find the
equivalent locus filter for each of the real filters. In Refs. [
24,
25] the CCTs of initial lights and their filtered counterparts are given, see Table
III for the filters in use. Then, the equivalent locus filters giving the same temperature change as the Wratten filters can be found by Eq. (
6).
Table III.
Initial and filtered colour temperatures for Kodak filters as specified by Kodak, and equivalent locus filter temperatures.
| Filter | Initial CCT | Filtered CCT | LTF of equivalent locus filter |
|---|
| 80A | 3200 K | 5500 K | −7652 |
| 85 | 5500 K | 3400 K | 8905 |
| 81 | 3510 K | 3400 K | 108,491 |
| 82 | 3290 K | 3400 K | −101,691 |
Figure 9.
Spectral transmittance of Kodak Wratten filters in the study compared to their locus filter counterparts.
![]()
In Figure
9, we show the spectral transmittance of the four Wratten filters compared with their equivalent locus counterparts. The locus filters are normalized so that the maximum transmittance of each is equal to the maximum transmittance of the corresponding Wratten filter. We can see that locus filters have similar transmittance behavior compared to the Wrattens, but they tend to be smoother in shape. This is particularly apparent for the case of color balancing filters (Figs.
9a and
9b). In the case of light balancing filters, the difference between the Wratten ones and their locus counterparts is less apparent (Figs.
9c and
9d).
Let us now consider how the 4 Wratten filters and their companion 4 equivalent locus filters behave when they are used to filter lights. We will consider the filtering behavior for 3 sets of lights: the Granada daylights, the 102 illuminants compiled by Barnard et al. [
26] which includes many artificial lights, and the set of 81 Wien-Planckian lights (from 2000 K to 10,000 K in 100 K steps). For the color conversion filters 80A and 85 (and their locus filter equivalents) we subdivide each illuminant set into two subsets. Filter 80A is designed only to make warm colors cooler so we consider how it changes the CCT of a light when it is applied only on illuminants that have an initial CCT that is less than 5000 K. Conversely, filter 85 is designed to make cool colors warmer. For this filter we will consider only the lights that have a CCT higher than 5000 K. All lights are considered for the light balancing filters 81 and 82 since they are designed only to make small alterations in the CCT.
In order to compare the behavior of Wratten filters to their equivalent locus ones we use three metrics: the change of CCT after applying the filters, the distance in
u,
v space to the Planckian locus,
Duv, and the color rendering index (CRI
Ra) of the filtered light. For the latter, we adopt the CIE 1995 method for its calculation, which is based on the color difference between standard samples rendered with the light source and the same samples rendered using an ideal light source with the same color temperature as the first one. Tables
IV—
VII report the mean CCT shift, the mean
Duv and the mean CRI
Ra when applying the Wratten filters, 80A, 85, 82, and 81, respectively, and their equivalent locus filters for the 3 sets of light. As expected, the shifts in CCT are small for the light balancing filters 81 and 82. In addition, the magnitude of the mean shift is consistent for these two Wratten filters and their equivalent locus ones. Higher mean CCT shifts are reported in the color conversion filters: 80A and 85. Here we see that the filter 85 (which makes light warmer in appearance), on average, performs like a locus filter regarding CCT shifts. However, the filter 80A, which makes lights cooler, on average, does not perform like a locus filter.
In terms of Duv, one can observe that these distances are relatively small and coherent between Kodak and locus cases for light balancing filters (81 and 82). However, in the case of color conversion filters, 80A performs slightly better than the locus filter in maintaining the distance between the filtered light and the locus when applied on Granada daylights. But it works less well for the Planckians and the Barnard set. The locus filter performs better than filter 85 for the 3 sets of illuminants.
Regarding color rendering indices, the light balancing filters 81 and 82, unsurprisingly given their small CCT change, make lights with similar indices as the unfiltered lights and this is also true for the equivalent locus filters. However, for the larger CCT changes induced by filters 80A and 85 the means values of color rendering indices change markedly and are generally significantly worse and yet for the equivalent locus filters the—on average high—color rendering indices are maintained.
Table IV.
Average CCT shift, Duv and CRI Ra changes after applying the Kodak Wratten filter 80A and its equivalent locus filter.
| CCT shift | Duv | CRI Ra |
|---|
| 80A | Locus | Unfiltered | 80A | Locus | Unfiltered | 80A | Locus |
|---|
| Planckians (ct < 5000) | 6101 | 3650 | 0 | 0.006 | 0 | 99.8 | 90.7 | 98.7 |
| Granada (ct < 5000) | 15,198 | 7410 | 0.003 | 0.003 | 0.004 | 94.9 | 87.7 | 96.4 |
| Barnard (ct < 5000) | 5855 | 3694 | 0.005 | 0.009 | 0.005 | 81.8 | 85.2 | 83.9 |
Table V.
Average CCT shift, Duv and CRI Ra changes after applying the Kodak Wratten filter 85 and its equivalent locus filter.
| CCT shift | Duv | CRI Ra |
|---|
| 85 | Locus | Unfiltered | 85 | Locus | Unfiltered | 85 | Locus |
|---|
| Planckians (ct ≥ 5000) | 3756 | 3686 | 0.001 | 0.010 | 0 | 98.1 | 92.3 | 99.9 |
| Granada (ct ≥ 5000) | 3010 | 2898 | 0.002 | 0.010 | 0.002 | 95.7 | 89.3 | 95.4 |
| Barnard (ct ≥ 5000) | 3609 | 3552 | 0.005 | 0.007 | 0.004 | 95.9 | 92.0 | 95.6 |
Table VI.
Average CCT shift, Duv and CRI Ra changes after applying the Kodak Wratten filter 81 and its equivalent locus filter.
| CCT shift | Duv | CRI Ra |
|---|
| 81 | Locus | Unfiltered | 81 | Locus | Unfiltered | 81 | Locus |
|---|
| Planckians | 349 | 407 | 0 | 0.001 | 0 | 98.7 | 98.8 | 98.8 |
| Granada | 334 | 408 | 0.002 | 0.002 | 0.002 | 95.6 | 95.5 | 95.6 |
| Barnard | 316 | 373 | 0.005 | 0.005 | 0.005 | 90.0 | 89.9 | 89.9 |
Table VII.
Average CCT shift, Duv and CRI Ra changes after applying the Kodak Wratten filter 82 and its equivalent locus filter.
| CCT shift | Duv | CRI Ra |
|---|
| 82 | Locus | Unfiltered | 82 | Locus | Unfiltered | 82 | Locus |
|---|
| Planckians | 450 | 525 | 0 | 0 | 0 | 98.7 | 98.7 | 98.6 |
| Granada | 361 | 408 | 0.002 | 0.002 | 0.002 | 95.6 | 95.9 | 95.7 |
| Barnard | 424 | 491 | 0.005 | 0.005 | 0.005 | 90.0 | 89.9 | 90.0 |
To conclude, we have found that the light balancing filters, in terms of their filtering behavior when applied to Wien-Planckian, filter lights like locus filters. However, color conversion filters filter lights somewhat differently from locus filters. Indeed, when conversion filters are applied to both Wien-Planckian and real lights they do not maintain, as well as locus filters, the distance to the Planckian locus.
Of course, looking at Fig.
9 we see that the light-balancing filters are quite neutral in color, very smooth and very close, spectrally, to their locus filter counterparts. So, we expect them to filter lights like locus filters. In contrast, the color conversion filters are designed to make larger changes in correlated color temperatures and are designed to be used under specific lighting conditions. Moreover, that they do not filter lights like a locus filter must be related to their relative non-smoothness, again see Fig.
9.
5.
Conclusion
The locus filters have the property—unique over all and any other formulations of transmissive filter—that they map any Wien-Planckian to another Wien-Planckian with a different color temperature. In this work, it has been shown that a locus filtered daylight is another daylight spectrum and the shift in its correlated color temperature is similar to that induced in the equivalent Wien-Planckian light. A key result that follows from our analysis is that we are able to solve for daylight spectra using a simple and elegant formula (that is much simpler than the standard daylight spectrum calculation). In detail, our corrected daylight, for a given correlated color temperature, is simply a filtered Wien-Planckian having the same temperature. The optimal correction filter—that best maps Wien Planckians to corresponding standard daylights—is determined by optimization.
Significantly, our new corrected-filter formula for daylights has an additional advantage that it also works for daylights with a CCT less than 4000 K. The set of corrected daylights induces a new daylight locus in the u,v chromaticity diagram. Our new locus is very similar to the existing daylight locus but it extends to warmer colors.
Empirically, we also showed that the CCTs of real daylights (not on the daylight locus) filtered by locus filters shift as predicted by our locus filter formulae. Moreover, when a daylight is not on the daylight locus the set of chromaticities generated for a range of locus filters (making lights cooler and warmer) effectively generates a per illuminant locus which on average runs parallel to the daylight (and Planckian) locus.
Finally, we examined the extent to which 4 Kodak Wratten filters filtered lights like equivalent locus filters. The equivalent locus filters for the Wrattens inducing a significant CCT change were found to filter real and artificial lights more consistently. That is, the locus filtered lights maintained their color rendering indices (Whereas the Wratten filtered ones did not) and the locus filtered lights better maintained their relative positions with respect to the Planckian locus.
 Find this author on Google Scholar
Find this author on Google Scholar Find this author on PubMed
Find this author on PubMed
 Open access
Open access