Creating a robust design of the spectral sensitivity of a color measuring device such as a camera, scanner, or colorimeter requires several considerations. These include accounting for existing optical elements in the design such as lenses, IR filters, and sensor quantum efficiency; realizability of color filters; recording illumination; variability of spectral characteristics in manufacturing; and system noise. In the design and evaluation of these devices, it is efficient to use a figure of merit (FOM) or goodness measure that is closely correlated with perceived color accuracy [1–9]. The FOMs are usually developed to obtain high correlation with various ΔE averages in the CIELAB color space. The advantage of using an FOM is that its computation is considerably less than simulating the average ΔE over an ensemble of spectra under realistic noise conditions. Of course, as we show, the development of effective FOMs requires such simulations. Once the FOM is developed, it is easy to use it to compare different devices or even optimize them.

Typically in formulating a camera design problem, a mathematical model is used for the device imaging process such as the following where the visible spectrum has been mathematically sampled at N wavelengths [10]. The N × M dimension matrix H contains the M spectral sensitivities of the device that we wish to design; the diagonal matrix O contains the concatenated spectral sensitivities of the other elements of the device (e.g., lens, IR filter, sensor efficiency); the N-element vector r represents the radiant spectrum that is measured by the device; the M-element vector n is zero mean, additive noise; and the M-element vector c is the value measured by the device. To simplify things, we will combine the matrix H and the matrix O into an N × M matrix G, giving us Note that the radiant spectrum r entering the camera can be broken down into an illuminant and a reflectance component. The illuminant is of importance when considering the mapping to CIE values.

To facilitate the design process, we wish to quantify the goodness of the overall system spectral sensitivity given by the matrix G. Such a goodness measure, can be used to determine a matrix H that provides the “best” color measuring results. Depending upon the approach, the matrix H is analytically determined with constraints on realizability (e.g., nonnegativity, smoothness) [11–15], parametric models (e.g. Gaussian shapes) [2, 4, 16, 17], or selected from a set of readily available filters  [8, 18, 19]. Regardless of the approach used, the use of a measure to quantify how well a filter set performs relative to the goodness measure is of use.

Here we compare how well different FOMs correlate to ΔE performance for a number of cameras. For each camera, simulated raw camera values of spectral samples are transformed to CIEXYZ values using the linear minimum mean square error estimator. The camera model includes signal dependent noise. In computing the ΔE value on each spectral sample, we average over a large number of signal dependent noise realizations. The resulting ΔE values from the spectral samples are averaged. The correlations are then computed between averaged ΔE and FOMs for the collection of cameras.

There are several measures that have been proposed to quantify the goodness of the spectral sensitivity of a color measuring device. These measures were developed to measure how well the device performs in providing accurate CIE color measurements obtained by the linear minimum mean square error (LMMSE) method. Using notation similar to above, the CIEXYZ vector for the radiant spectrum r can be expressed as where the N × 3 matrix A contains the sample CIEXYZ color matching functions, and the three element vector t(r) is the CIEXYZ value of the radiant spectrum r. Again this radiant spectrum can be decomposed into an illuminant and reflection component, and the illuminant will define the white point to which we would map to CIELAB. In this work, we assume a spectrally uniform illuminant. There are measures that consider multiple illuminants [3] as well as work that considers the problem of capturing data for multiple illuminants [12]. Here we are focused on comparing measures of goodness for a single illuminant.

The earliest measure for quantifying the goodness of a single color filter m is Neugebauer’s q-factor [20]. Mathematically, this measure is given by where PA is the orthogonal projection operator onto the subspace defined by the matrix A. The projection operator can be determined from The q-factor is bounded between 0.0 and 1.0, with a value of 0.0 indicating that the filter m lies totally outside (is orthogonal to) the subspace defined by the CIE color matching functions and 1.0 indicating that the filter lies completely inside the subspace. Note that the q-factor only provides the measure of a single filter. This single filter constraint is a shortcoming of the q-factor, as we require a measure that quantifies the entire system response that is defined by the matrix G in Eq. (2). For example, we could select three filters that are each contained in the subspace defined by matrix A giving optimal q-factor values of 1.0 for each filter. However, when the filters are combined, it is possible that they do not span the full three-dimensional subspace defined by the matrix A.

The Vora value [21] solves this issue and is given by where PG is the orthogonal projection operator onto the subspace defined by the system response that we wish to quantify, and can be computed in the same manner as Eq. (5). Similar to the q-factor, the Vora value ranges from 0.0 to 1.0 with 0.0 indicating that the subspaces defined by the matrix A and G do not overlap (are orthogonal) and 1.0 indicating that the subspaces are the same. The Vora value does not consider the spectral data that is being measured, nor does it account for system noise. Sharma proposed several FOMs that account for these parameters [5]. Sharma assumes the use of a LMMSE estimator in his FOMs.

The most complex FOM proposed by Sharma is given by where the denominator is given by and Sr is mathematically defined below and is an autocorrelation matrix related to the reflectance or radiant spectra, but in the perspective CIELAB color space.

The numerator is given by where Sn is mathematically defined below and is a weighted version of the noise autocorrelation matrix. The symbol ⊗ represents the Kronecker product.

To complete the definition of the FOM, the autocorrelation matrix terms are given by where JF(t(r)) is the Jacobian matrix of the transformation to CIELAB space for the CIEXYZ value t(r).

Note that the above FOM requires the statistical characterization of the ensemble of spectra {r}, assumes signal independent noise, and also assumes that a minimum linear least squares estimator is used for mapping the measured value to CIEXYZ values. In this FOM, through the use of the Jacobian matrix, a first order Taylor approximation is made at each reflectance value to account for the transformation to CIELAB from CIEXYZ, which provides a perceptually more meaningful measure. Such an approximation was introduced by Wolski for the design of color filters [14]. See Appendix C of Sharma [5] or Eq. (4) of Wolski [14] for details on computing the Jacobian.

In practice, the noise model for a color measuring instrument is not signal independent but is signal dependent. While the noise is signal dependent, it is uncorrelated with the signal. The recorded measurement value can be well modeled with a Poisson distribution [8, 16, 22]. A characteristic of a Poisson distribution is that its mean is equal to its variance. In our case, due to the large number of photons that arrive at the sensor, we can model the mean value as the noise-free measurement, and the noise as a Gaussian distribution that has a zero mean with a variance that is a scaled factor of the measured value. The scaling occurs due to the existence of gain in the system. A system gain of γ on a measured component will scale the noise-free value by γ but scale the variance by γ2, introducing a scale factor of γ between the Poisson mean and variance. It is straight-forward to determine the scale factor for a particular device through the measurement of known reflectance samples [22]. Figure 1 provides an example case, where a Nikon D750 camera was used to measure samples of spatially constant reflectance. Here we plot the mean value of the sample versus the variance within the sample. The slope of the linear fit to the data (shown as a red line) indicates the scaling factor (γ value) that should be used for the noise model for a channel of the camera, which is approximately γ = 0.4 as shown by the fitted line in the figure. It is common to see scale factors of γ = 0.4 to 0.8 in cameras that we have investigated.

It is possible to adjust the FOM given in Eq. (7) to account for a signal dependent noise model. The adjustment involves performing a modification of Eq. (11). Instead, we use where n(r) represents the realization of a signal dependent noise value when measuring the radiant spectrum r. Note that the variance of the noise is dependent upon the value of r. The value Ssd is used in place of Sn in the computation of the value for τ given in Eq. (9).

In practice, the values of Ssd, Sr, and Sn are estimated from an ensemble of selected spectra. Assuming that we have a collection of P spectra, estimates for each of these terms are given by and where Kn(ri) is the autocorrelation matrix of the noise when measuring the radiance spectrum ri. When computing the value of S̃sd, the autocorrelation matrix Kn(ri) is known from the camera model. For example, if the M channel noise slopes due to the system gain are given by γ=[γ1,…,γM]T and is the noise-free measurement, then where ⊙ represents the Hadamard product, and diag(. ) is an operator that creates a diagonal matrix from a vector.

In addition to accounting for signal dependent noise, it is useful if an FOM is linearly related to the ΔE performance of the device. Sharma noted that the FOM he developed has a 1−FOM relationship to ΔE, which is clearly nonlinear [5]. To achieve a measure that linearly relates to ΔE performance, we can apply a correction factor to the FOM measure that is given by This correction ensures that the measure remains between 0.0 and 1.0 with a value of 0.0 indicating a poor measure and a measure of 1.0 indicating a perfect measure. This same adjustment was suggested by Quan et al. where they altered Sharma’s FOM measures to account for cross illumination mappings [3].

Given the above measures, our focus is to compare their ability to quantify the color accuracy of a camera. To investigate this, we used two data bases of camera spectral sensitivities, and four spectral reflectance/radiance data sets. The sensitivity data bases consisted of a database from RIT [23] that contained 28 cameras and a database of 20 phone cameras [24]. The spectral databases include reflectivities of a textile database [25] (4827 samples), an X-Rite SG chart (140 samples), a Digieye DT chart (240 samples), and a set of radiant spectra measured in situ (2262 samples) [26]. We computed ΔE values that resulted from the LMMSE method for each data set with each camera for a level of signal dependent noise that was given by a scale factor of 0.8 in each of the color channels. In this computation, we used the LMMSE estimator that was based upon the known components of the device model. The signal dependent noise model was handled in the same manner as was used in Trussell and Shamey [27]. It was not necessary to perform a regression data fit, since the model components are known exactly. Note that we used ΔE and not ΔE2000 as the error metric. The reason is that the Jacobian matrix JF( t(r)) used in Sharma’s original measure does not account for the weighting that is used in the computation of the ΔE2000 error metric. At this point, we want to use Sharma’s original calculation, which assumes a uniform error weighting in the CIELAB components.

These average ΔE values for each camera are compared to the previously discussed FOMs. To do this, we computed the Vora value for each camera. In addition, we computed the FOM value given by Eq. (7) for each camera and data set combination assuming signal independent noise given at a level that was the average of the signal dependent noise across the data set. Finally, we computed the new FOM measure that accounted for signal dependent noise (using Eq. (16)) and included the nonlinear adjustment. For completeness, and to enable the ability to determine the usefulness of accounting for signal dependent noise, we also computed the original FOM value given by Eq. (7) but with the nonlinear adjustment applied to it, to provide a linear relationship to ΔE. To compute the ΔE performance of each camera, it is necessary to run a large number of noise simulations. We used 1000 noise realizations for every spectral sample across all the cameras.

We present the results in several different plots. Figure 2 shows how the Vora values of the cameras relate to the simulated ΔE performance for each of the spectral data sets. The dashed line is the least squares linear fit to the data. From these plots, we see that the Vora value struggles in providing a clear relationship to ΔE. While there is one outlier camera that clearly has poor performance in terms of ΔE and the Vora value, the remaining cameras show limited correlation between ΔE and the Vora value. Many cameras result in the same Vora value but have significantly different average ΔE performance numbers. While useful for cases where there is no spectral information about the data being measured, it may not be as useful for cases that employ such information. For our remaining comparisons, we will remove the outlier camera, since all the FOMs also identified the camera as producing very poor colorimetric accuracy.

Figure 3 shows the results of using Sharma’s FOM as it was originally defined for the four spectral data sets. The FOM and ΔE axes have the same scaling to indicate dependency of the FOM on the data sets. Figure 4 show the same results but with the nonlinear adjustment applied to the FOM values. As before, we show the least squares linear fit to the data. In addition, the correlation coefficient for each fit is provided. The FOM values show an improvement compared to the Vora values in terms of having a correlation with ΔE. Comparison of the correlation coefficients between Figs. 3 and 4 show only a slight improvement obtained by the application of the nonlinear adjustment. Comparison of the four data sets show that the in situ data set [26] FOM results (both adjusted and non-adjusted) are quite different in nature from the other three data sets. In addition, the correlation coefficient is lower for the in situ data set, implying the discrimination of cameras with different ΔE performance numbers is not very good in Fig. 4(d).

Figure 5 shows the results when using the FOM that accounts for signal dependent noise, which involves the use of Eq. (16). The results are quite good for all four spectral data sets in that the slope of the relationship between the FOM and ΔE are similar, and all have high levels of correlation. Fig. 4(a)–4(c) are similar to Fig. 5(a)–5(c) in terms of their correlation numbers. A clear difference exists though for the in situ data set. The in situ data looks good when we account for the signal dependent noise (Fig. 5d) compared to the case that assumes a signal independent noise model (Fig. 4d).

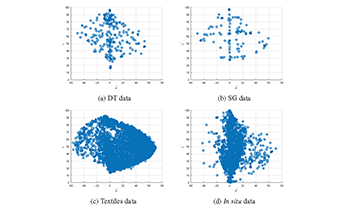
The difference between Fig. 4(d) and Fig. 5(d) prompted an investigation into the source of the difference. It was found that the in situ data set includes samples that contain relatively dark luminance values, which are not present in the other data sets. Figure 6 displays CIELAB gamut cross sections of the four data sets. From this figure, we can see that the in situ set of Fig. 6(d) contains a number of spectra with L∗ values below 15 (approximately 5% of the spectra). These are dark compared to the black values in the color targets and textiles. Examination of these spectra showed they could have relatively high values in the UV and IR ends of the spectrum, but little in the visible range covered by the CIE color matching functions.

Investigation of the difference between S̃sd and S̃n for the in situ data set showed that Sharma’s FOM estimates a significantly lower SNR for the dark samples compared to the measure that accounts for the signal dependent noise. The signal independent average noise produces a very low SNR for the dark samples that affects the estimation process and degrades the overall FOM. As such, it ends up relating poorly to the ΔE values that occur with the signal dependent noise model. To demonstrate the issue, we removed dark samples (those with L∗ < 15) from the in situ data set and computed the original FOM (with the nonlinear adjustment) with the version that uses S̃sd. The results are shown in Figure 7 which show similar levels of correlation. We also verified the dark sample effect by adding 5% dark spectra to the textiles database, which resulted in the standard FOM measure to perform poorly.

This work investigated how well goodness measures for the spectral sensitivity of color measuring devices relate to color performance. The approach considered a realistic camera model that included signal dependent noise, which is dominant in virtually all cameras. It was shown that the Vora value does a poor job in relating to ΔE. It was also shown that Sharma’s FOM has issues if the spectral data set includes samples that have low luminance levels. Use of an FOM that accounts for signal dependent noise was shown to help improve the correlation with ΔE performance, in particular if the device is to be used for a wide range of luminance values. This signal dependent noise FOM should prove useful in the determination of optimal spectral responses for color measuring devices and in comparing the colormetric performance of different devices.