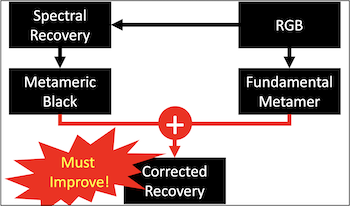
The Matrix-R decomposition teaches that, with respect to a set of sensors, any spectrum can be written as the sum of its fundamental metamer—in the subspace spanned by the spectral sensitivities of the camera—and a metameric black (orthogonal to the camera spectral sensitivities). In any RGB-to-spectra recovery algorithm we might expect a good spectral recovery to have the property that, when projected onto the RGB sensors, it equals the RGB from which it was estimated. Or, equivalently, the fundamental metamers of the ground-truth and algorithm-recovered spectra should be equal. In this paper, we make this expectation more concreted and present an elementary proof that this “Matrix-R-compliance” post-processing step must always improve the RMSE (root-mean-squared error) accuracy of any RGB-to-hyperspectral recovery algorithms. Further, we consider and rework the proof for the case where the spectral data is known to live in a basis of small finite dimension. Experimental results are presented for three historic RGB-guided hyperspectral pan-sharpening algorithms. Here the algorithm input includes a high-spatial-resolution RGB image and a low-resolution hyperspectral counterpart. We show the evidence that the RMSE accuracy of all tested algorithms are improved by this Matrix-R-compliant process, while we also find the best recovery results from adopting a low-dimensional linear model that models the variation of spectra in a scene.