Previously improved color accuracy of a given digital camera was achieved by carefully designing the spectral transmittance of a color filter to be placed in front of the camera. Specifically, the filter is designed in a way that the spectral sensitivities of the camera after filtering are approximately linearly related to the color matching functions (or tristimulus values) of the human visual system. To avoid filters that absorbed too much light, the optimization could incorporate a minimum per wavelength transmittance constraint. In this paper, we change the optimization so that the overall filter transmittance is bounded, i.e. we solve for the filter that (for a uniform white light) transmits (say) 50% of the light. Experiments demonstrate that these filters continue to solve the color correction problem (they make cameras much more colorimetric). Significantly, the optimal filters by restraining the average transmittance can deliver a further 10% improvement in terms of color accuracy compared to the prior art of bounding the low transmittance.

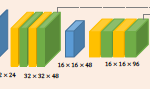
Most cameras still encode images in the small-gamut sRGB color space. The reliance on sRGB is disappointing as modern display hardware and image-editing software are capable of using wider-gamut color spaces. Converting a small-gamut image to a wider-gamut is a challenging problem. Many devices and software use colorimetric strategies that map colors from the small gamut to their equivalent colors in the wider gamut. This colorimetric approach avoids visual changes in the image but leaves much of the target wide-gamut space unused. Noncolorimetric approaches stretch or expand the small-gamut colors to enhance image colors while risking color distortions. We take a unique approach to gamut expansion by treating it as a restoration problem. A key insight used in our approach is that cameras internally encode images in a wide-gamut color space (i.e., ProPhoto) before compressing and clipping the colors to sRGB's smaller gamut. Based on this insight, we use a softwarebased camera ISP to generate a dataset of 5,000 image pairs of images encoded in both sRGB and ProPhoto. This dataset enables us to train a neural network to perform wide-gamut color restoration. Our deep-learning strategy achieves significant improvements over existing solutions and produces color-rich images with few to no visual artifacts.

The performance of colour correction algorithms are dependent on the reflectance sets used. Sometimes, when the testing reflectance set is changed the ranking of colour correction algorithms also changes. To remove dependence on dataset we can make assumptions about the set of all possible reflectances. In the Maximum Ignorance with Positivity (MIP) assumption we assume that all reflectances with per wavelength values between 0 and 1 are equally likely. A weakness in the MIP is that it fails to take into account the correlation of reflectance functions between wavelengths (many of the assumed reflectances are, in reality, not possible). In this paper, we take the view that the maximum ignorance assumption has merit but, hitherto it has been calculated with respect to the wrong coordinate basis. Here, we propose the Discrete Cosine Maximum Ignorance assumption (DCMI), where all reflectances that have coordinates between max and min bounds in the Discrete Cosine Basis coordinate system are equally likely. Here, the correlation between wavelengths is encoded and this results in the set of all plausible reflectances 'looking like' typical reflectances that occur in nature. This said the DCMI model is also a superset of all measured reflectance sets. Experiments show that, in colour correction, adopting the DCMI results in similar colour correction performance as using a particular reflectance set.

In Spectral Reconstruction (SR), we recover hyperspectral images from their RGB counterparts. Most of the recent approaches are based on Deep Neural Networks (DNN), where millions of parameters are trained mainly to extract and utilize the contextual features in large image patches as part of the SR process. On the other hand, the leading Sparse Coding method ‘A+’—which is among the strongest point-based baselines against the DNNs—seeks to divide the RGB space into neighborhoods, where locally a simple linear regression (comprised by roughly 102 parameters) suffices for SR. In this paper, we explore how the performance of Sparse Coding can be further advanced. We point out that in the original A+, the sparse dictionary used for neighborhood separations are optimized for the spectral data but used in the projected RGB space. In turn, we demonstrate that if the local linear mapping is trained for each spectral neighborhood instead of RGB neighborhood (and theoretically if we could recover each spectrum based on where it locates in the spectral space), the Sparse Coding algorithm can actually perform much better than the leading DNN method. In effect, our result defines one potential (and very appealing) upper-bound performance of point-based SR.

We describe a comprehensive method for estimating the surface-spectral reflectance from the image data of objects acquired under multiple light sources. This study uses the objects made of an inhomogeneous dielectric material with specular highlights. A spectral camera is used as an imaging system. The overall appearance of objects in a scene results from the chromatic factors such as reflectance and illuminant and the shading terms such as surface geometry and position. We first describe the method of estimating the illuminant spectra of multiple light sources based on detecting highlights appearing on object surfaces. The highlight candidates are detected first, and then some appropriate highlight areas are interactively selected among the candidates. Next, we estimate the spectral reflectance from a wide area selected from an object's surface. The color signals observed from the selected area are described using the estimated illuminant spectra, the surfacespectral reflectance, and the shading terms. This estimation utilizes the fact that the definition domains of reflectance and shading terms are different in each other. We develop an iterative algorithm for estimating the reflectance and the shading terms in two steps repeatedly. Finally, the feasibility of the proposed method is confirmed in an experiment using everyday objects under the illumination environment with multiple light sources.

The internal structure of the snow and its reflectance function play a major contribution in its appearance. We investigate the snow reflectance model introduced by Kokhanovsky and Zege in a close-range imaging scale. By monitoring the evolution of melting snow through time using hyperspectral cameras in a laboratory, we estimate snow grain sizes from 0.24 to 8.49 mm depending on the grain shape assumption chosen. Using our experimental results, we observe differences in the reconstructed reflectance spectra with the model regarding the spectra's shape or magnitude. Those variations may be due to our data or to the grain shape assumption of the model. We introduce an effective parameter describing both the snow grain size and the snow grain shape, to give us the opportunity to select the adapted assumption. The computational technique is ready, but more ground truths are required to validate the model.

With the rapid development of display technology, the colour mismatch of the colours having same tristimulus values between devices is an urgent problem to be solved. This is related to the wellknown problem of observer metamerism, caused by the spectral power distribution (SPD) of primaries and the difference between individual observers' and the standard CIE colour matching functions. An experiment was carried out for 20 observers to perform colour matching of colour stimuli with a field-of-view of 4° between 5 displays, including two LCD and two OLED, against a reference LCD display. The results were used to derive a matrixbased colour correction method. The method was derived from colorimetric visually matched colorimetric data. Furthermore, different colour matching functions were evaluated to predict the degree of observer metamerism. The results showed that the correction method gave satisfactory results. Finally, it was found that the use of 2006 2° colour matching function outperformed 1931 2° CMFs with a large margin, most marked between an OLED and an LCD display.

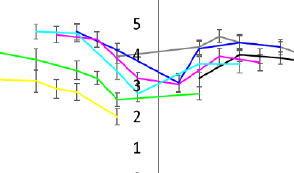
A psychophysical experiment was carried out to investigate visual comfort when reading on three OPPO Find X3s displays at three luminance levels (100, 250 and 500 cd/m2) at five illuminance levels (0, 10, 100, 500 and 1000 lx). Twenty young observers evaluated visual comfort using a 6-category points method. The results showed that observers felt most comfortable at the illuminance of 500 lx or display luminance of 500 cd/m². There was an interaction between ambient illuminance and display luminance. High ambient light and display brightness levels provide a more pleasant visual experience. In low ambient light, however, the lower the brightness level, the more comfortable it is to see. Regarding the influence of background colour on visual comfort, the observers felt more comfortable having a grey background than white or black colour. When at dim illuminance, the background colour would have a great influence on visual comfort for negative contrast conditions, but when at higher illuminance, different background lightness levels had a great impact on visual comfort for positive contrast conditions. The above findings are very similar to the display luminance levels of 100 and 250 cd/m².

The human visual system is capable of adapting across a very wide dynamic range of luminance levels; values up to 14 log units have been reported. However, when the bright and dark areas of a scene are presented simultaneously to an observer, the bright stimulus produces significant glare in the visual system and prevents full adaptation to the dark areas, impairing the visual capability to discriminate details in the dark areas and limiting simultaneous dynamic range. Therefore, this simultaneous dynamic range will be much smaller, due to such impairment, than the successive dynamic range measurement across various levels of steady-state adaptation. Previous indirect derivations of simultaneous dynamic range have suggested between 2 and 3.5 log units. Most recently, Kunkel and Reinhard reported a value of 3.7 log units as an estimation of simultaneous dynamic range, but it was not measured directly. In this study, simultaneous dynamic range was measured directly through a psychophysical experiment. It was found that the simultaneous dynamic range is a bright-stimulus-luminance dependent value. A maximum simultaneous dynamic range was found to be approximately 3.3 log units. Based on the experimental data, a descriptive log-linear model and a nonlinear model were proposed to predict the simultaneous dynamic range as a function of stimulus size with bright-stimulus luminance-level dependent parameters. Furthermore, the effect of spatial frequency in the adapting pattern on the simultaneous dynamic range was explored. A log parabola function, representing a traditional Contrast Sensitivity Function (CSF), fitted the simultaneous dynamic range data well.