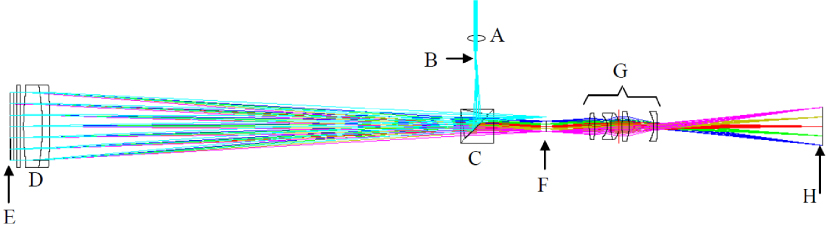
In a computer-generated holographic projection system, images are generated via the controlled diffraction of coherent light, which is modulated by a spatial light modulator (SLM). Contemporary SLM’s can only modulate either phase or amplitude, hence algorithms are needed to compute amplitude-only or phase-only holograms. Among those, phase-only holograms are generally preferred due to inherently higher energy efficiency as there is no intentional blockage of light during modulation. Classic phase retrieval algorithms include direct binary search [1], simulated annealing [2], Gerchberg-Saxton [3], and recent years have also seen numerical optimization methods [4–8], but these methods are iterative so computation speed is the major challenge. Previous studies have demonstrated a real-time computer-generated holography (CGH) method called one-step phase retrieval (OSPR) [9], which was fast enough for real-time holography, but the reconstruction quality still has potential for improvement. Hence, a computationally inexpensive method is needed to improve the reconstruction quality whilst maintaining the real-time property of the OSPR algorithm.

There are several factors contributing to the non-linearities between the reconstruction of hologram and the target image, including the calculation and quantization of the hologram, modulation of the light and imperfections in the optical setup. This article proposes the digital pre-distorted one-step phase retrieval (DPD-OSPR) algorithm. The digital pre-distortion (DPD) is carried out on the holographic projection system using holograms computed by the OSPR algorithm by measuring the non-linearity experimentally and applying the corresponding pre-distortion curve on target images. DPD can be done via a one-to-one correction curve or a lookup table (LUT) which allows the relationship between the input and output to be adjusted without any heavy computation.

The intuition of the proposed DPD-OPSR algorithm for CGH comes from the gamma correction method for conventional displays, such as cathode-ray tube (CRT) monitor [10], plasma display panel television (PDP-TV) [11] and thin-film-transistor liquid-crystal display (TFT-LCD) [12, 13]. Gamma correction for conventional displays were originally developed to mimic the perceptual response of human vision [14]. The work presented here is a logical continuation of this approach applied to holographic displays.

The DPD-OSPR method builds on the OSPR algorithm [9]. The OSPR algorithm relies on the time multiplexing of holograms, exploiting the response time of eyes in order to reduce noise in the replay field, rather than computational optimization of the hologram. As the random noises are averaged by the eye while the target image stays, the perceived noise is lessened by the temporal average detected by the eye [15].

The OSPR algorithm is described in Algorithm 1, where the propagation function P is simply the Discrete Fourier Transform (DFT) for Fraunhofer diffraction [16]. The number of subframes S is set to 24 in this study. The OSPR algorithm generates each hologram subframe by taking the inverse Discrete Fourier Transform (iDFT) on the field concatenating the target image with a random phase, and then the phase-only constraint is applied by discarding the amplitude while keeping the phase. After computing the S subframes, they are then displayed on the SLM sequentially. For real-world SLM with limited bit depth, a further step of quantization on each subframe is needed.

The holographic projector used in this experiment is a Fourier projection system developed by Freeman [17], as shown in Figure 1. The design consists of a diode-pumped solid-state (DPSS) 532 nm 50 mW laser source, focussed down by an aspheric singlet (A), the focus of which becomes the diffraction limited point source (B) for the projector. The beam then passes through a polarizing beam splitter cube (C) to a collimating lens (D), which illuminates the SLM (E). The SLM is a binary phase SXGA-R2 ForthDD ferroelectric Liquid crystal on silicon (LCOS) micro-display with a refresh rate of 1440 Hz, a pixel pitch of 13.6 μm and a resolution of 1280 × 1024. An aperture at point (F) spatially filters out the other orders, leaving only one first order, which is then magnified up by a finite conjugate lens group (G) to produce an image, of the required size, on the screen (H) [17].

The mechanical components are listed in Figure 2 with parts numbered. The holograms displayed on the SLM are generated using the OSPR algorithm [9], and as the SLM is a binary-phase modulator, each hologram subframe needs to be binary quantized. Then each group of the 24 binary-phase hologram subframes are encoded as the 8-bit red, green, blue (RGB) channels of a 24-bit image to interface with the SLM driver electronics. The SLM displays each bit plane sequentially, with ones and zeros mapping to opposing phase modulations at each pixel. The reconstructions were captured using a Canon 550D camera with an EFS 18–55 mm lens. To ensure fair comparison, the camera was set to the same manual setting when comparing each pair of replay fields before and after DPD. It takes 24∕1440 = 1∕60 s to display all 24 subframes on a 1440 Hz SLM, so the camera shutter speed was set to 1∕30 s to capture all frames twice. The images captured are raw format in RGB colour, which are subsequently converted to grey-scale (using the rgb2gray function in Matlab [18]) when calculating normalized mean squared error (NMSE) against the target images, using equation NMSE =1n∗∑(x−x̂)2 ∑(x)2, where x is the target, x̂ is the measured output and n is the dimension of x and x̂.

To determine the DPD curve of the holographic projection system, the non-linearity needs to be measured first. The hologram in Figure 3(b) was first generated using OSPR algorithm for the linear grey-scale ramp of pixel value increasing linearly from 0 to 255, as shown in Fig. 3(a), along with a single pixel white (255) strip at the left end as a fiducial marker to demonstrate the beginning of the grey-scale region [15].

The projection output of the linear grey-scale ramp was then captured and cropped as shown in Fig. 3(c), from which the non-linearity curve was determined, by averaging each column of pixels in the image and discarding the fiducial marker, forming the blue line in Fig. 3(d). A third-order polynomial fit was applied, generating a smoothed non-linearity curve (yellow line in Fig. 3(d)).

A high degree of non-linearity is exhibited. By taking the mean of the square of the error between the measured output (blue line) and the linear reference (green dashed line), the normalized mean squared error (NMSE) of the measured output was calculated to be 0.0858. To correct for the non-linearity, the DPD curve (red line) was formed by inverting the smoothed non-linearity curve (yellow line) in Fig. 3(d).

Subsequently, the DPD curve (red line in Fig. 3(d)) was used to adjust the grey-scale ramp, achieving the pre-distorted grey-scale ramp as shown in Figure 4(a). The corresponding projection output was then captured as shown in Fig. 4(c). By using the same method of averaging columns of pixels, the measured output was plotted in Fig. 4(d). It can be seen that the corrected non-linearity was much closer to linear comparing to the original non-linearity, and the NMSE was calculated to be 0.0039.

Thus, as demonstrated in Table I, DPD achieved a 95.45% reduction in MSE, which was a significant improvement in non-linearity, therefore the DPD curve measured is validated.

To qualitatively demonstrate the effectiveness of our approach, we project a simple test pattern of a graduated ramp test pattern consisting of 10-step strips in Figure 5(a), which is commonly employed in gamma-correction calibration of many display systems. As shown in the projection replay field captured in Fig. 5(c), before DPD, the right few strips are barely distinguishable. In comparison, after carrying out DPD, it can be seen that each pair of adjacent strips in Fig. 5(f) are much more distinguishable, qualitatively showing the effectiveness of the DPD method.

Then the DPD curve was applied to the two sample images as shown in Figure 6 (a) and (b), producing pre-distorted images in Fig. 6 (c) and (d). Holograms were generated for each image using the OSPR algorithm and loaded onto the SLM respectively. The corresponding replay fields were captured as shown in Figure 7.

The replay fields of the holographic projection of original images are shown in Fig. 7 (a) and (b), and the replay fields of the holographic projection of images after DPD are shown in Fig. 7 (c) and (d).

As shown in Fig. 7(a), it can be seen that, before DPD, the edges between the buildings and the sky were quite ambiguous, with most detail of the sky being lost. In comparison, after DPD, the replay field in Fig. 7(c) provided not only sharper edges between buildings and the sky, but also more detail of clouds in the sky. The NMSE of the replay field for sample image 1 decreased from 0.06139 to 0.04920, which was a 19.86% reduction.

In Fig. 7(b), before DPD, the horse was difficult to distinguish from the background, especially around the horse’s back area. But after DPD, as shown in Fig. 7(d), contrast has been significantly boosted and the fine detail around this part of the horse is more evident. The NMSE of the replay field for sample image 2 decreased from 0.04309 to 0.03635, which was a 15.64% reduction.

Hence, as summarised in Table II, DPD achieved a 19.86% reduction in NMSE for sample image 1 and a 15.64% reduction in NMSE for sample image 2, quantitatively proving the effectiveness of DPD method for CGH of real-world test images using OSPR algorithm.

Finally, as the DPD is a one-to-one mapping, the computation time is negligible. In practice, the computational overhead is too small to be measured against randomness between subsequent runs. DPD can also be further accelerated in hardware using a hardware LUT, so that the DPD can be carried out instantly. This approach is widely adopted in gamma correction for displays.

The non-linearity between target image and reconstructed image was measured for the overall holographic projection system by projecting a linear grey-scale ramp. Then DPD was applied to the grey-scale ramp and successfully reduced the MSE by 95.45%. To examine its effectiveness on real-world images, the DPD method was applied on two sample images, it was observed that more details were shown in the replay field after DPD, and the MSE’s of the two example images were reduced by 19.86% and 15.64%. As the DPD is a one-to-one mapping, the extra computation required is negligible. Thus, we have demonstrated the effectiveness of the proposed DPD-OSPR method to improve reconstruction quality on the existing OSPR algorithm while still keeping its ability for real-time holography.