Regular
A 
Audio degradationsappearance of blacksAutomotive ImagingAUTOMATIONAPPLICATIONS OF STEREOSCOPIC DISPLAYSART GALLERYAmmonia DetectionArt, aesthetics, and emotionanti-counterfeit label classificationAppearance segmentationAERIAL SURVEILLENCEautoencoderARTIFICIAL INTELLIGENCEactivation functionsartist’s color wheelaerosol contaminationAcceptance and AnnoyanceAutonomous driving (AD)Antireflective coatings (ARC)Ambient lightattention connectionapplications of stereoscopic displaysAction recognitionAdaptive background modelsatmospheric point spread functionAction Recognitionagent-based simulationACTIVITY RECOGNITIONAppadaptive data cubeAR engineARTWORKSAdaptive Context EncodingART TRAININGActive learningasynchronous operationattentional stanceADVECTIONAttentionALEXNET MODELAliasingAsynchronousalgorithmic artAnomaly detectionaugmentationAutomotive imagingAdverse Weatherautonomous vehicle imaging systemsAppearance controlappearance measurementactive pixel sensor APSARauto-tuning hyperparametersADAPTABILITYAutomated Driving SystemAlfa-RootingAIAOM/AV1and True 3D DisplaysArtificial intelligenceatomic number estimationAutomated VehiclesAppearance preservationART PERCEPTIONADMMACADEMY COLOR ENCODING SYSTEMAutomaticArtistic ResearchAlternating minimizationAppearance reconstructionATTRIBUTES SELECTIONAUTOSTEREOSCOPIC TWO-VIEW DISPLAYAudio qualityArtistic Image QualityAuto white balanceaerosoAPP PERMISSIONSAlignmentattributionARTATTENTIONACCUMULATED RELATIVE DENSITY (ARD)AutonomyActuation methodANALOGUEAutonomous vehiclesaerial displayAMBIENT AND FOCAL VISIONantibacterialAUTONOMOUS VEHICLEaesthetic measureALGORITHMS AND METHODOLOGIESActivity ClassificationARCHIVAL MODELActivity timeAFFINE TRANSFORMAutoencodersautomated testingART VIEWINGADAPTIVE STEGANOGRAPHYAV1Aesthetic EnhancementAssistance systemappearanceAPPLESCRIPTANCIENT CHINESE TEXTILEArtifact Repairassistive devicesAMBIENT LIGHTACCEPTABLE RANGESAUTO WHITE BALANCEAUTOMATED MACHINESAutomatic Image Quality Optimizationaddressing climate change, environment, quality monitoring, surveillancealgorithm-driven visualizationAdditive manufacturingAutomotive cameraambient lightingAttention mechanismaugmented visionautostereoscopyabsolute value kernelASTROPHOTOGRAPHYAESTHETICSAutonomous Vehicle SystemsauthenticationARRAY CAMERAadjustable block spaceAUTONOMOUS VEHICLESANDROID APP TESTINGAstrophysicsARCHIVEAPS/CCD DEFECTS RATESAUTO CONTROLadditional JPEG compressionADASADF SCANNERAGENT-BASED SIMULATIONADAS/AD DomainAPPLICATIONSARIMAABR streamingArt Forgeryambient lightingsaddressing Climate ChangeAutomotive perception systemACESADC AND OTHER IMAGE SENSOR BLOCKSatmospheric scattering modelauthentifityAppsANDROID KEYLOGGERapp developmentAMERICAN FOOTBALLAdvanced Driver Assist SystemsAncient DocumentsAnomaly Segmentationautomatic document sequencingair–liquid interfaceACTIVE PIXEL SENSOR APSARTIFACTSAccess Controlaffective responses to visual sensationsABSORPTANCE PREDICTIONAPPEARANCE DECOMPOSITION AND RECONSTRUCTIONadaptive denoisingARCHAEOLOGYAutomotiveAutonomous Vision SystemsADDITIVE MODELadaptive image filteringassessmentautomated facial detectionAUTONOMOUS DRIVINGart historyAutonomous SurveillanceAUDIOVISUALAutonomous VehicleAppearance ReproductionAutomatic colorizationAccelerometer sensorAUSTRALIAN SERIES SYSTEMAppearance ModelAdaptive Video Streamingautomotive applicationAdditive ManufacturingApproximate Bayesian InferenceADAPTIVE FRAME RATEAdaptive focusaccelerometerautomatic detectionAlgorithmAdaptive filteringabnormal operation behaviorAugmented realityADCAttention DisruptionAuto exposureassistive technologiesart, aesthetics, and emotionaccessibleALTREF_FAMEAmerican footballAUTOENCODERautostereoscopic printAPS DEFECTS RATESautomotive cameraADJUSTMENT SCALING METHODOLOGYassimilationanalysisART, AESTHETICS, AND EMOTIONAttribute certaintyAPS defects ratesALPHA SHAPESartificial IntelligenceAUGMENTED REALITYAdaptive DisplayAerial floating imageABSORBING MEDIUMAppearance ordering systemAOIAnnoyanceANNAge effectARCorearchiveAUTOSTEREOSCOPIC 3D DISPLAYAmbient IlluminanceAutoencoderAccelerated agingabsorptionAutomatic ISP tuningAutostereoscopic DisplayAdaptive Image ProcessingANDROID SECURITYalgebraic reconstructionAttitude determinationART EXPERIENCEArtificial neural networkArtificial IntelligenceAuto-flashAUTOSTEREOSCOPYautomated Windows system monitoringautonomous vehiclesAdversarial TrainingADC and other image sensor blocks, photodiodes, pixels, and processesAnaglyph captureART & SCIENCEanthropometryACRalpha-trimmed random forestaliasingASILAmbient-awareADAS (ADVANCED DRIVER ASSISTANCE SYSTEM)AUDIO-VISUAL QUALITYaction recognitionAVMAcceptabilityAutonomous Vehicle-to-Pedestrian communicationADDITIVE MANUFACTURINGAffective computingartAuscultationAffineART & PERCEPTIONAssistive TechnologyautocorrelationARTIST-FRIENDLY TOOLAIRBAGadditive manufactureAudioartificial intelligenceApertureARCHIVINGADAPTIVE SURROGATE FUNCTIONSAutomated Machinesaperture modeanisotropic gradientArt AuthenticationALBERS' PATTERNautonomous systemsAUTOFOCUS IRREGULARITYAPPEARANCEartificial neural networksalarm systemattacksABSOLUTE AND RELATIVE DEPTHAmbient LightingAperiodicAgingAutomatic white balanceAssistance systemsAcutanceAutocorrelationanalysis-ready dataAsian Lacquerautomatic exposure controlAppearance-basedADVANCED COLOR CONCEPTSaudio degradationsALPHA-ROOTINGAnalyticsaesthetic perceptionADAPTIVE CODING STRUCTUREAlgorithmic artAWGNautomatic identificationAdversarial examplesAugmented RealityAOMAggregationAviation Maintenance Technician (AMT)ArchivingArt HistoryAutomatic parameter tuning methodart trend analysisAdversarial attacksAphantasiaAutomated DrivingASYMMETRIC DISTORTIONauto-focusingAND PROCESSESAudiovisual archivesAESTHETIC PERCEPTIONadviceApodizationattention mechanismAnnihilating FilterACUTANCEautomated testing deviceAPS/CCD defects ratesactive contourautomated vehiclesAUTOFOCUSADDITIVE REGULARIZATION OF TOPIC MODELSANODIZED TITANIUMautomotive displaysAdversarial networkanalysis of time series dataAFADJUSTED SELF-EXEMPLARAGGREGATESanomaly detectionAPPEARANCE MODEAncient Studiesaudio-visual qualityAdversial Erroraccurate emotion tagADAPTIVE OPTICSAutomotive simulatoraccessaerodynamicsAcademy Color Encoding SystemAccess SystemsAutonomous drivingAdvanced Driver Assistance SystemAccelerationASICacousticadvanced driver assistance systemAGE ESTIMATIONAnomalous behavior identificationAssistanceAppearanceaggregation-induced emissionautonomous drivingautonomous vehicleautonomous flying projectorARABIC CHARACTER RECOGNITIONautomatic curriculum generationAudio signal classificationAktina VisionApplications of Stereoscopic DisplaysAUTOMOTIVE DESIGNautonomousAUTOFOCUS SPEEDAdvanced Driver Assistance System (ADAS)ADC and other Image Sensor BlocksareaarchivingADC and other image sensor blocksacidolysisAUTONOMOUS WHEELCHAIRADAPTIVE SKIN DETECTORacetateAnalogue PhotographyAutonomous CarsASYMMETRIC MATCHINGAUTOMATION SERVICESASTRO-CHEMISTRYautosomal polycystic kidney diseaseArtist RecognitionALGORITHM REDUCINGAUTO EXPOSUREautostereoscopicacousto-opticAugmented Reality (AR)automotiveANDROID APP SECURITYAutonomous VehiclesAdvanced driving assistance systems (ADAS)alkoxideADAPTIVE PREDICITONaerial imageaudiovisual archiveartist identificationAntidepressant pharmacotherapyannotationsArtist materialsaestheticsauto white balanceancient manuscriptambient contrastAngular candidateAI performance metricsAutomatic data labelingAerial image analysisarcheological textilesAugmented Reality headset with eye tracking capabilitiesAUDIO UNDERSTANDINGAndroidautostereoscopic displayALL IN FOCUS IMAGINGaugmented realityauditionArtAdversarial Attacksaccelerated agingAUDIOAPPSAudio Captchasairflow visualizationaesthetic qualityADDITIVE MANUFACTUREAnomaly DetectionAR deviceABYSS COLORAudiovisualARTIFICIAL SCOTOMAAUTONOMOUS NAVIGATIONAutonomous DrivingAgglomerative clusteringAGINGActive LearningACTIVE LEARNINGaerial work vehiclesactive learningAdaptive Radial DistanceAPPROXIMATIONADAPTIVE TONE MAPPINGangular resolutionAuthenticationAutomobileAESTHETICS QUALITY PREDICTORARCHIVESATTRIBUTE-BASED ENCRYPTIONARCHIVAL CONTROL
B 
BRDFbio-inspired networksBINARY DESCRIPTORBundle AdjustmentBRANCHLESS DISTANCE DRIVEN PROJECTORSblind imbalanced domainsBinocular colorBrightness effectBRDF measurementsBlindnessbooksBlockchainbipartite graphB-GANBag-of-Features (BoF)BRAIN CONNECTIVITYbiosensorbrdf modellingbiometric identifierBRDF AcquisitionBrightnessBehavior Recognitionbackground luminanceBACKGROUND COLORBRDF simulationsBilayer DielectricBatch SteganographyBANDINGBound magnetic polaronBATTERY LIFEboundary equilibrium GANBinocular visionBrightness compressionBinary ClassificationBORDER LUMINANCEBinningBokeh effectBETWEEN SUBCARRIERS (ICI)BINARY PIXEL PATTERNSBLIND IMAGE QUALITY ASSESSMENTBI-REFLECTANCE DISTRIBUTION FUNCTIONBlind image watermarkingBacklitBlenderBoundary DetectionBokehbandingBrillianceBayesian networkbilateral filterBGA packaged chipsBiometricsbanding artifact removalBio VisualisationBLACKMAGIC PRODUCTION CAMERABoard gamesBILIRUBINBODY GESTURESBlind detectionbackwardbindingBright ambientBlurring Edge Widthbig dataBRDF modelingBayesian estimationBIDIRECTIONAL REFLECTANCE DISTRIBUTION FUNCTION (BRDF)Bloodblind and low visionBidirectional LSTMBONE SEGMENTATIONBESTBOTTOM-UP FACTORS OF THE SCENEbiobankBoundary layerbuilding evacuationbiometric quality assessmentbrainBLURRED CONTOURSBIG GRAPHSBusiness-oriented interaction rulesBase augmentationblendshapeBackside illuminated pixels (BSI)behavior analysisBISPECTRAL DONALDSON MATRIXBuilding waste SortingBody motion analysisBlind quality metricsBackground-awareBOOSTED LOCAL FEATURESBayesian Deep LearningBlue Teambackground subtractionBASELINEblurBrain Computer InterfaceBIOMECHANICSblind estimationBONE AGE ASSESSMENTbenchmarkingborder controlBONE AGEBand noiseBLOCK MATCHINGBio sensorblindnessBLURRINESSblind noise spectrum estimationbarcodeBODY IMAGEblind noise level estimationBehavior PredictionBackground SubtractionBehaviourBLACK-BOX MODELb-splinesbrush stroke analysisBhattacharyya distanceBIORTHOGONAL WAVELETSBENCHMARKBayesian modelingBRIGHT PUPILBinary imageBACKGROUND ESTIMATIONBig DataBipartite FieldBACKGROUNDBed Exitbig data analyticsBarcode DecodingBTFBLUE BALANCEBIOFUELBiological Dynamic NetworksBlank paperBirdsBLOCK DIAGONALIZATIONBAND PASSbird populationBrush particleBarcodeBandingBSSRDFBIG DATABLOOD PULSEBINARY-SHIFTBokeh adapterblinking rateBM3DBarcode DetectionBRISQUE ScorebrightnessBOKEHBLOCK-MATCHINGBACK-RAYCASTINGBiomechnical strainBRIGHTNESSbiomedical imagingBayesian cue reweightingblack and white filmBINOCULAR VISIONBenchmarkingBlind noise parameters estimationBFBLIND DETECTIONBACKGROUND CLEANINGBody verificationBackground estimationBody Progress Tracking SystemBuilding interiorsBAYERBlock matchingBaggage screeningBlock Chainbrightness perceptionBACKGROUND SUBTRACTIONBLIND ESTIMATION OF NOISE CHARACTERISTICS
C 
COLOR ARTIFACTSCONTRAST ENHANCEMENTCamerasCOATINGScamera IDCLUSTERED-DOTCROWDSOURCINGCOMPUTER GRAPHICSCrimeCOLOR SPACECOUNTERFEITING GOODScolor fidelityContent complexitycolor similarityColour harmonyCOUPLED DICTIONARY LEARNINGCLARITYCritical Infrastructure Protectioncomputer graphics pipelineCOMPUTER FORENSICScorrection modelCOLORIMETRIC ERRORComputer GraphicsCOMPUTER GENERATED HOLOGRAMCT reconstructionCCDCOMPLEX DOMAINcoaxial optical systemsComputer VisionCYBERSICKNESSCIRCULANT MATRICEScmos image sensorsCorrelationClustering MethodColor accuracyCOLOR PALETTEScomputational artConditional FingerprintsCONTENT-BASED IMAGE RETRIEVALCamera AlignmentContraction MappingCOLLECTION DEVELOPMENTCOLOR MATCHINGcolor filter arraysComparative EvaluationCELLMICROCOSMOScomputer visionCriminial forensicsCOMPRESSIVE LIGHT FIELD DISPLAYClusteredcyber securitycloud architectureCPIQCIELABCritical Flicker FrequencyCYBERFORENSICSCorrelation predictorCausticCOMPOSITE MATERIALScolor image appearancecataract operationsCHANGE DETECTIONCOVID-19Convolutional Neural Networks (CNN)Contrast Detection ProbabilityCOMPUTATIONAL MODELINGCOLOUR PREFERENCEConvolutionCAMERA TUNINGCHATBOTcyber sicknessCo-DesignCollision perceptionCOMPUTER VISIONcolor perceptionCOGNITION RESEARCHCompressionColour Appearance ModelCattle Keypoint Detectioncrisis responseCIELAB Color SpaceCORNER DETECTIONCONTEXTcolor scienceCULTURAL HERITAGEChartCROSS-CONTENT COMPARISONSColor Appearance Modelcolor shiftCROSSENCODERSColor reproductionCinematographic workColorimetricCamera Image QualityCorresponding colourcomposition optimizationcolor profilingCalibrationcolor associationContrast Signal to Noise Ratio (CSNR)cognition researchCIECAM16 Colour Appearance ModelCONSTRAINED RECONSTRUCTIONcellphone imagerscross polarizationcentroidCamera SystemCircularCHILDREN WITH CHRONIC HEALTH CONDITIONSCamera calibrationConditional GANCHEMOTHERAPYCNNsCODING EFFICIENCYcycloramaCylindrical color modelCONE-BEAM MBIRCurvatureColour correctioncloud servicescultural heritageCHROMATIC CONFOCAL SENSORCOUNTERFEIT DETECTIONChannel attentionCOLOR MANAGEMENTcamera color correctioncyber-securityCMOS Image sensorCONSUMER IMAGESCSFCanon Hack Development Kit (CHDK)CMFcreative intentcontouringcalibration 3d printingContent characterisationCollision envelopeconnected component analysiscartographyConvolution Neural Networkcultural heritage documentationCOMPRESSION ARTIFACT REDUCTIONConvolutional Neural Networks (CNNs)CEREBRAL ANEURYSMcolor adaptation transformCOLLABORATIVE TRAJECTORY VISUALIZATIONCattle Re-Identificationcalibration targetsConvolutional neural networks (CNN)Computational BokehColor Matching Functionscapacitance calculationCAMERA PIPELINECONSTRUCTIVE SOLID GEOMETRYCutting edge evaluationColour reproductionConvex Mirror Arraychange bitrateCMOS IMAGE SENSORcomplexityCOLLEGE FOOTBALLcolor representationCONVOLUTION NEURAL NETWORKCancer Detectioncontrast detectionCOMPUTATIONAL ILLUMINATIONCOLORIMETRYcerebellumConvolutional neural networkcollaborationCXR imagesCATALOGINGcolorfulnessCamera fingerprintCOMPUTATIONAL MODELColour reproduction workflowcontext mechanismColor Image Processingchroma keycontourlet transformcontrast enhancementConsumer Electronics MarketCOLOR AND LIGHT DESIGNcombined metricsClient-servercomputational visionColor Filter ArrayCOLOR SPOT DETECTIONcolor wheelcupping spotscybersecurityChecksumcomputed tomographycompetenciesColor CheckerConvolutional neural networksCyclopean imageCLANECosmologychemometricsCryo-Electron Microscopy (Cryo-EM)color deficiencyColored fabricated objectComplex measures of contrastCMFsCOMMON COLOUR APPEARANCEcracks detectionCOLOR DIFFERENCECAMERA MODEL IDENTIFICATIONCorrelated Multiple SamplingCoded apertureCOLOR IMAGECOLOR QUALITY FOR HIGH DYNAMIC RANGE COLOR CONTRASTCommunity Research Partnershipcorporate designCamera sensorColour appearance modelColor DeficiencyCOLOR SEGMENTATIONColo EducationCertificate of AuthenticationCrotch HeightConvolutional Neural NetsColor deficiencycomputer graphicscrowdsourcingcomplementary colorsCONTINUOUS TONECOMPLEXIONCamera imaging performance & image qualityCMOS image sensors (CIS)CONDUCTIVE FILMcolor spacecomputer vision, and remote sensing in food and agriculture systems: Farm, Livestock, Production, RestaurantcognitionCT SLICE IMAGEcolor sensationCOLOR LINEScolor photographyColor predictionCOSTCNNCarbon MonoxideContrast Sensitivity Functioncharged dropletscapture softwareCompressed sensingCustomer Content Defect DetectionCOLOR CORRECTIONComputational photographycomputational imagingCorrelated multiple samplingCOMPUTATIONAL SIMULATIONSCOLLABORATIVE CREATIVITYcolor segmentationColor directioncomputational modelCAVECIRCUIT -CONDUCTIVITY PATTERNchromatic aberrationcolor interpolationcontrast sensitivity functionColor Selection ToolCISCOLOR APPEARANCE MODELCONTEXTUAL EFFECTSContrastive LossCandlelightcolor correctionClusteringcomputational modellingColorimetryConvolution Neural Network safety systemcolor matchingcolour constancycolor visioncontrast detection probabilityCOMMUNITYCoral Reefcolor universal designCase studies and empirical studiesColor transformationclusteringCovid-19CHEWING DETECTIONConvolution Neutral Networkcolor demosaicingcloud manufacturingCADchromaticity gamutCNC printingcolour namingCHDK (CANON HACK DEVELOPMENT KIT)Clickstream datacameraComputational AnalysisContrast Transfer AccuracyConvolution Neural NetworksCOGNYSISComputer-generated integral imagingColor volumeComputer-Supported Experiential LearningClosed heightmap estimationCOORDINATE DESCENT METHODcontrast matchingcontour stereogramCrosslinkable Dopant-Receiving LayerCONNECTIONIST TEMPORAL CLASSIFICATIONCOLOR WARPINGCOLOR FILTERCOMPUTATIONALcolorimetric characteristicsCOLOR CALIBRATIONCORRUGATED PACKAGINGcollection assessmentCAMERA SPECTRAL SENSITIVITYColor perceptionCOLOR PROPERTIESCAMERA RIGCARBOXYMETHYL CELLULOSECrime AnalyticsColor Appearance AttributesColor image enhancementColor interpolationColor Managementcultural heritage dataCamera ValidationCognitive SciencesCOLOR OPTIMIZATIONcomputational halftoneClickable PaperCybersecurity TrainingComplex domainCURVELET SPARSITYconvex optimizationcontrast visionCNC cuttingColor DetectionChatbotcontext understandingcolor accuracyconfusion-line mapchromatic aberration compensation (CIE2000)Camera quality assessmentColor ImagingcaptureColor FadingCensysCOLOUR HESSIANConservationcatalogingCOLOR HALFTONING ALGORITHMCONTEXTUALLY AWARECOLOR DISTANCECHARACTER RECOGNITIONCyber sicknessCamera sliderCattle ReIDChallenges and limitationsCNN-based video featuresColor managementCryptographyCurationCOLOR BLURcross-modalityCAMERAconstant hue lociclassification modelColor Separation ProbabilityCAPTURING SYSTEMCHIP SCALE PACKAGECOLOR QUANTIZATIONCross-modalCOLORIZATIONCAMERA SENSOR NOISECROSS MODALCOMPRESSED SENSINGCopy-move forgeryCIE L∗a∗b∗ color spaceColor appearanceColour ConversionCharacterisation modelCOMBINED METRICSCOLOR PERCEPTIONCraftComplexityCLOUD DETECTIONColor Perceptioncaptcha solvingChromatic adaptationCivil WarConvolutional Neural NetworkConvolutional Neural Network (CNN)causal convolutionconsistent colour appearancecomputer-assisted connoisseurshipCOLOR CORRECTION MATRIXConjugate GradientcataractsCLUSTER CAMERACOLOURCLASSIFICATIONCultural Heritage ImagingColor vividnessChevreul illusionColor ScissioningCIE color differenceCross-Media Colour ReproductioncolorColour Deficiencyctadecenyl succinic anhydrideContrast Sensitivity Functions (CSFs)Cascaded regressionChromatic adpatationCAMERA CHARACTERIZATIONcausal brain connectivityCAMERA-RENDERED IMAGESCOLLABORATIVE VIRTUAL ENVIRONMENTComputationCONTENT-BASED OPTIMIZATIONcomplementary colorCTP platesCOMPUTATIONComputational ImagingCONTENT BASED ADAPTATIONCLUSTERED-DOT PERIODIC SCREENColour vision deficiencyCOOK DISTANCECMYKcolor calibrationCOLOR CAMERAColour constancyCattle activity recognitionCRISPENINGcrowd analysiscolorimetric errorConditional generative adversarial networksCovert CommunicationConditional Image Synthesiscross-modalcolor captureCLIPPING|RAY TRACINGcolor managementcomputer image analysis of artConservation documentationcontamination-levels predictionCamera image quality tuningCOLOR VOLUMEcolor space conversionContinuous TrackingCT RECONSTRUCTIONConvolution neural networkCONTOURINGCHROMATIC ADAPTATIONCoverage optimizationCondition-based Maintenancecamera characterizationCell imagingcurve fittingChromebookcolor enhancementcomputationComprehensive Reviewcompositioncamera fingerprintCNN approachcamera sensor patterncamera calibrationCOLOR SPACESCloudColor image gradientCMOS image sensorComputer graphicscreativityCYBERSECURITYConvolutional Neural Networkscompact networksCollimator FixtureCrowdsourcingCOLORIZINGColor misregistration measurementcomputational color constancyColor filtersConnected Component AnalysisColour FilterColor visionCHARACTER RECOGNTIONCENTER SURROUNDCOMPUTATIONAL PRINTINGchromogenic filmCONVERGENCECattle identificationclove extractCameracolor deficientCOLOR REPRODUCTION QUALITYCamera-based Monitoringcolor demosaickingcolor inconstancyCrystal separationcolor gamutCIFARColor Correction Matrixcolor temperaturechromaticity shiftcultural assets identificationCIELAB color spaceCollision Warningcolor print fadingCANON POWERSHOTControl feedbackcomputerized color vision testCOLOR DIFFERENCEScolor image statisticsclean energyCyber Security ConsultingCELL PHONEScurvatureCONVOLUTIONCamera forensicsCOMPTON CAMERACOLOR IMAGE PROCESSING IN SPATIAL DOMAINCONTRAST RATIOcardinalityconditional image generationCLUSTER DOTCOLOR CONSTANCYCONDUCTIVE POLYMERcolor spacescanonical light sourcecostCompression AlgorithmsCollaborative Virtual environmentCDPCone crosstalkCamera designCYBERSECURITY AND FORENSICSColor ScienceCLASS SPECIFIC COLLABORATIVE REPRESENTATIONConvolutional neural network applicationsCadasterCARLA SimulationCrossmodal correspondencesColumn ADCCARDBOARD EFFECTcell densityCANON EOS 5D MARK IIICommanding PostCAMERA IMAGINGCamera colour characterisationCOLOR DISCRIMINATIONColor printComputed tomographyColor AppearanceCYANOBACTERIACOMPRESSIONcolor characterizationCorrelated Double SamplingCBIRCMY Sensorchange detectionColour MatchingCAMERA IMAGE PROCESSINGcultural-heritageCASCADED CONVOLUTIONAL NEURAL NETWORKcollege student usersCritical InfrastructureColor Reference SystemCONTRAST LIMITED HISTOGRAM EQUALIZATIONCOLOR CHANNEL RECONSTRUCTIONcritical infrastructureCOLOR INTERPOLATIONCOLOR UNIFORM BLOCKCOLOR FILTER ARRAYContextcybersecurity trainingCamera resolutionContinuous inkjet printingCLOUD COMPUTINGCover-Source MismatchCamera-Based VitalsCONTRASTCODED APERTUREcritical infrastructure maintenanceColor VisionCOLLECTIONS CAREConcurrent Two-factor AuthenticationColor FilterColor spacecolor renditionCSLBP FEATURESContrastive LearningCoordinated Multiple ViewsCUSTOMISED PACKAGINGCharacter recognitionColor Accuracycolor constancycctColorizationComputingContrast EnhancementCOLOR GAMUT MAPPINGCOLLISION AVOIDANCE SYSTEMConfinementComputer-aided diagnosiscost functioncolor apperancecolour appearance ratingsCAMERA ARRAYSCONVOLUTIONAL NEURAL NETWORKChromatic adaptationsCOLORColour matching functionsCORRELATIONCOLOR IMAGE PROCESSINGcontrastCIRCULAR CODED PAYLOADScamera toe-inCOLOR QUALITYComputational PhotographyCultural heritageCopyrightComputer visionCOVID-19 testingContinuous latent variablesCryptographic HashColor discriminationContrast sensitivityCAMERA POSE ESTIMATIONCupcakescamera performanceCIE LABCompressed Sensingcolor object recognitioncamera arrayColor Appearance Models (CAM)camera spectral sensitivityCAVE AlternativeCOLOUR HARRIScolor distributionCROSSTALKcomputer aided healthcareCopyright and Counterfeit of CNN weightsConsumer Electronicscost aggregationchromatic adaptationcolour characteristicsColor GamutCOLOR MEASUREMENTCOLOR SPACE CONVERSIONCONVEX OPTIMIZATIONCybersecurityCOLOR ERRORcharacter recognitioncolor appearanceCMOS Image SensorCoating failureCOLOR SEPARATIONCloud Deploymentcamera manufacturecolored filterCONDITIONCLUSTER TEXTURECORRELATION MEASURECOLOR WORKFLOWCUDACINEMATIC VRCoatingcybersecurity and forensicscolor profileCOLOR CONSTANCY DATABASEcolor patch reductionCattle recognitioncopy of heritage objectCOUPLING ANALYSISclass attentionColorfulness in tone mappingCNN-based classifiersconvolutional neural networkCONTRAST ENERGYCLASSIFIER ENSEMBLINGconvex hullColour-differencecolor bar codesCLUSTERINGcolor QR codecrop diseaseColor Difference Metriccalibration modelsCBAMcamera spectral sensitivitiesCPDCOLOR FILTER ARRAY OPTIMIZATIONcolor cameraCAMERA IMAGE QUALITYCaptureContrast sensitivity functionChromatic AdaptationConvolution Neural Network deploymentCELL PHONECINEMATIC VR CAPTUREcollection managementcyberbullyingCamera performancecamerasClimbingcontrol synthesisCALIBRATION TARGETCOLOR IMAGINGcultural differencesCONVOLUTIONAL NEURAL NETWORKScolor appearance modelsColor Universal DesignColor constancyCURVATURECOLOR APPEARANCECOLOR PROFILEColor gamutContrast Detection Probability (CDP)Contrast enhancementCOLOR VISIONcompressive sensingCIE LAB coordinatesCFAColour managementchromatic contrast sensitivityColour Matching Experimentscolour matching functionscolor correlated temperatureCOGNITIONcolor vividnesscontrast sensitivityComputational imaging and image processingCOLOR CHARACTERISTICCorresponding ColoursCOLOR CENTERContent Based Image Retrieval (CBIR)Cross Stage Feature Pyramid Network (CSFPN)channel attentionCultural Heritagecrowd congestionCoded diffraction patternsCALIBRATIONcamera color characterizationCOLLOIDAL CRYSTALCity ModelingCOPYRIGHTCIELAB color differencecolor differencecolor spatial processingcolor restorationcloud computingCamera PerformanceConvolution Neural Network Intellectual Property protectionColour OrderCAM02-SCDColor CorrectionCOLOR SEMANTICSConfocal MicriscopyCOLOR PREFERENCEcolor imagingComputer-generated hologramCamera spectral sensitivitycolour vision deficiencyCOMPUTER SECURITYCMOSchrominance histogramCAMERA QUALITYColourcamera pipelineCAMERA-PROJECTOR SYSTEMCHROMATICITYCanny algorithmCOLOR VISION DEFICIENCIESCMOS SENSORCIECAM16colorimetrychemical amplificationConstrained Convolutional Layercontact angleCIE Standardscolor reproductioncolour appearance modelCOLOR GAMUTcollimatorcamera angle estimationcrowd behaviorCounter-Drone systemcomputational photographyconditional GANsCOMPENSATION OF MOTION ARTEFACTScolor compositionCAMERA BENCHMARKINGCIE xy chromaticity diagramCharts, Diagrams, and Plotscolor categorizationCONTRAST SENSITIVITYCognitionCOPYRIGHT PROTECTIONcontext modellingCOLOR VISION DEFICIENCYColor correctionCamera pose estimationcolor namingCorresponding Colorscolor discriminationCOLOR TRANSFORMcoherent imagingCOLOUR APPEARANCE MODELcritical infrastructuresCareaboutsCYBER SICKNESSComputational artCOLOR REPRODUCTIONcolor noisecolor facial image representationClassifiercolor pipelinecalibrationcultural heritage and conservation applicationscationic photopolymerizationCryo-electron microscopyCOLOR EXTRACTIONcorrelated multiple samplingcircular codingColour Matching FunctionsCritical flicker frequencyCURVED OBJECTCMOS Image SensorsCROSS-PLATFORMcredibility weightingCOMPUTATIONAL PHOTOGRAPHYCybersecurity and ForensicsCMTcompressionCAMERA CALIBRATIONCryptographic hashingComparative Visualizationconvolutional neural networksCHARACTERIZTIONColor errorcategorical colourchromophore mapschromacross-modal associationconformancecrosstalkCultural heritage objectsCAMERASCIEClassificationCOPY SENSITIVE GRAPHICAL CODEScorresponding colorClassification of vehiclesCMOS IMAGE SENSORScontrast sensitivity function (CSF)coated cardboardcommunityCONTRAST RESOLUTIONCamera obscuraCOMPUTATIONAL IMAGINGColor quantizationcolor volumeColoured point cloudCyber-securityClustered microcalcificationsCONSUMER VIDEOcoherent diffraction imagingChabotCAMERA COLOR PROCESSINGCORRELATION IMAGE SENSORComparative analysisCNN (CONVOLUTION NEURAL NETWORK)Counterfeiting CurrencyCNN deep learningcolor analysisCONVOLUTIONAL FEATURESCARS microspectroscopycultural heritage and conservation applications: perspective analysisColor Measurementcomputational art analysisCROSS TALKcloud securityCHI-SQUARE SIMILARITY MEASURECONTENT-ADAPTIVECyber SecurityCOLOR ACCURACYCamera ModuleChange DetectionCloud-based ApplicationColour Space Optimisationcolor unmixingcarnauba waxCOLOR DIFFERENCE THRESHOLDCitation StatisticsClinical Pathwaycolor stabilityColorblindness testconvolutional neural network (CNN)Color ReproductionCrane classificationColorCamera Monitor System (CMS)Camera phone image qualityCMY Color Filtercollaborative filteringcomputer image analysis of art (paintings, prints, drawings)CT IMAGE RECOGNITIONcamera resolutioncolor workflowCANONcompositional metricconfusion metric
D 
device integrationDepth estimationdigit extractionDeepfake DetectionDykstra's projection algorithmDepth EncodingDIGITAL WATERMARKINGDisplay systemsdecoding rate estimationdynamic programmingdigital displayDriving AutomationDIGITAL HALFTONINGDeep Neural networksData acquisitionData augmentationDeep Learning Image Quality Assessment NoiseData-parallel primitivesDALTONIZATIONdisplay technologyDriver Assistance SystemData VisualizationDeepfakeDIGITAL FABRICATIONDigital color cameraDEEP CONVOLUTIONAL NETWORKdirect binary searchDigital HeritagedigitizingDocument Visualizationdigital artsDashboardDisruptive TechnologyDEPTH SENSOR ARCHITECTUREData ThroughputDegraded imageDeepSortDISTRIBUTED PROCESSING SYSTEMDesign EngineeringDISTURBANCE COMPENSATORDEMdetection of vehiclesDNNDriving simulationdynamic range compressiondetection theoryDIGITAL PRINTINGDIGITAL SIGNAL PROCESSORDimension ReductionDark Matter Simulationsdual-energy x-ray CTDIGITIZATION STANDARDSDynamic FeaturesdesignDukeMTMCdiscrete cosine transformDeepFakesdigital museumdepth-dependent filteringDriver Monitoring SystemDatabasesDE-RENDERINGdisplay characterization modelData Glovedual-band filterdigital healthcareDIMENSION REDUCTIONDolby VisionDepth Mapdatabase film-makingdiscontinuity indicatordata miningDISCRETE COSINE TRANSFORM (DCT)Deep neural networkDigital CamerasDead LeavesDriver MonitoringDENTAL MATERIALData MiningDenoising efficiencyDYNAMICSDEMOSAICINGDynamic Vision SensorDEGRADED IMAGERYDMDDomain Knowledgedigital archivingDual tree complex wavelet transformDATA ASSOCIATIONDepth sensorDisparity Mapdisparity estimationDocument Image Quality AssessmentData fusiondirection gradientsdeuteranopiadisplay analysisdischargeDynamic resolutiondigital curationDriver AssistanceDISOCCLUSION ARTIFACTSDIVERGENCEDisplayed tabletDisplacements and strains monitoringDXOMARK MOBILEDynamic|stereodelentropyDigital Halftoningdictionary learningDigital PhotographyDIVISIVE NORMALIZATIONdriving safetyDemosaicdielectric objectsDisparity calculationDialogflowdetectiondense SIFTDrowsiness detectionDISPLAY RESOLUTIONDYNAMIC RANGE COMPRESSIONdynamic rangeDocument Authenticationdirect brightness matchingDONATIONSDeep LearningDistribution Shift in ImagesDeep Neural Networkdrug efficacyDefect DetectionDigitizationDigital watermarkingdepth of fieldDeep neural networksDisplacementsdeep learningDepth CompressiondigitizationDocument securityDICTIONARY LEARNINGDEPTH ORDERDual-energy CT imageDRIVING AUTOMATIONDOWN-SCALING AND TILINGDEPTH FROM FOCUSDimension reductiondepth perceptionDatabaseDUAL CONTOURINGDEPTH OF FIELDDifferentiable rendererdwell timeDehazingdomainDANGEROUS DRIVING EVENT DETECTIONdynamic multi-viewDEPTH PERCEPTIONdeep learning networksDEHAZINGDEEP NEURAL NETWORKDeep learningdatasetDental resin compositesDirect binary searchDenoisingData EmbeddingDEGRADATION IDENTIFICATIONDiscomfortDEEP LEARNINGDEPTH CAMERADSPDisplay Technologiesdata modelingDigital image forensicsDISTRIBUTIONDigital LibrariesDeepFake Detection MethodsDISPARITYDisplay and Viewing ConditionsDeltaICtCpDisplay WallDownload StatisticsDUAL LIGHTING CONDITIONDepth Image-Based RenderingDECLARATIVEDRIVER MONITORING SYSTEMDATA FUSIONDIGITAL TAGDifferentDATASETDEPTHdata volume reductiondata fidelity gradientDisplay Image-BarcodesDISCRETE FOURIER TRANSFORMDARK CURRENTDOCUMENT IMAGE ANALYSISDCTRDTWdeep image priorDepth Image Based RenderingDensity map reconstructionDigital accessibilityDILATED CONVOLUTIONSDeep feature extractionDCIDEAD LEAVESdual energy CTDynamic Vision SensingdenoisingDATA MINING AND ANALYTICSDocument Reading SequenceDIMENSIONALITY REDUCTIONDeepFakeDomain AdaptationData AugmentationDISPARITY ESTIMATIONdistant viewingDriving-specificdigital cameraDIGITAL PRESERVATIONDIGITALDeconvolutionDirectional lightDeep face featuresDigital forensicsDimensionality reductionDescreeningDISTINCTNESS OF IMAGEdeep neural networkDomain adaptationData compressionDECISON TREE MODELdifferent colour backgroundDigitization/3D imagingdeep networkDIGITAL DENIMDeblurringDISCRIMINATIVE RANDOM FIELDDIBR SYNTHESIS VIEWdrawing trainingdata augmentationDYNAMIC RANGEDataset generationDigital image annotationDeep learning featuresDIGITAL HOLOGRAPHIC DISPLAYDigital fabricationdigit inferenceDynamic Temporal DataDIDMCDIY networkingDRUNK DRIVINGDepthDeceptionDiscrete wavelet transformdrawingDigital restorerDeep Neural NetworksDigitisationdepth estimationDEBLURRINGDisplayDIGITAL COLLECTIONSDIFFRACTIONDigital Holographydisplay metrologydeveloping printerdigital halftoningDirect SolvingDiffractionData visualizationDiffractive optical elementDOCUMENT CLASSIFICATIONDOIdata renotationDARK SHOT NOISEdata fusionDiscriminatordisplaydepth mapdepth predictionDEEP-LEARNINGdouble mirror systemDUAL-CAMERADISCRETE COSINE TRANSFORMdisaster response robotDiffraction LimitDIFFERENT COLOR CENTRESdeepfakeDiffractive imagingDEGRADATION TYPEDeep-learningdiffractive optical elementsdifferent electromagnetic rangesDistributed TrainingDIGITAL MAP PROCESSINGDEEP NEURAL NETWORKSdepth discriminationDepth mapsDeformable registrationdiscounting illuminantDigital Watermarkingdiluted magnetic semiconductorsDepth perceptionDeepfake videosData-driven approachdense predictionDISPLAY BANDWIDTHdata analysisDiffuse MaterialDUPLEX HALFTONE PRINTSDETECTOR CASCADEDaltonizationDigital rear view mirrorsDynamic ScenesData AnalyticsDIGITAL PRINTING ON COTTONdarknet marketplacesDIGITAL FILM CAMERARED SCARLET CAMERADark Channel PriorDelaydeep convolutional neural networksDesign studyDeep convolutional residual networkdigital watermarkingdiode efficiencyDESIGNDISPERSIONDISPLAYSData set fittingDiffuse lightingDIVING VIDEOdiminished realityDiverse sourceDiscrete Cosine Transform (DCT)DATA REDUCTIONDegradation parameterdistortiondataset correctionDISTANCE JUDGEMENTDXOMARKDEMOSAICING ALGORITHMDRIVE RECORDER IMAGEdepthdifference curvatureDEPTH ESTIMATIONdigital photographyDIGITAL FORENSICSDIFFUSE LUNG DISEASEDISPLAY GAMUTdecision-makingData AnalysisDYNAMIC SAMPLINGDISTORTION COMPENSATIONDeep Reinforcement LearningDigital ArchivingDepth Estimationdata analyticsDukeMTMC-reIDdead leaves chartDetection probabilitydataset generationDISCRETE COMPUTATIONAL IMAGINGDigital restorationDRONEdigital signageDual-energy CTDISPLAYDUAL-ENERGY CTDISTRACTED DRIVERSDevice identificationDIGITIZATIONDiffraction CompensationDeep featuresdynamic color mappingData associationdigital collectionsDemosaicingdata annotationDEPTH EXTRACTIONDRIVER ASSISTANCE SYSTEMdetectability indexdisaster managementdye amount estimationDEVICE GAMUTDigital microscopyDRAM Memory BandwidthDrowsiness DetectionDepth Perception AssessmentDISPLAY QUALITYDEFECT PIXEL CORRECTIONData StreamsData annotationdeep neuralDETECTIONDTGDxOMark Mobiledigital literacyDepth informationDeepfake detectionDisaster AnalysisDEPTH-COMPRESSIONDriving behaviorsdiagnostic imagingdepth imageDistance teaching/learningDigital Art Historydeep neural networksDistraction DetectionDEFOCUS MAPDENOISEdigitalisationDEGHOSTINGdata managementDUST HEALINGDigital PreservationDIFFUSE LIGHTINGdepth reconstructionDATA AUGMENTATIONDual-energy x-ray imagesdiffusion tensor imaging (DTI)Datasetdepth sensitivityDE-DISPERSIONDistributed Deep Learningdegree of adaptationDisplay ScienceDot gaindata modelsDiscrete CoordinatesData hidingDIGITIZATION KITDOCKER CONTAINERSdriver facial feature recognitiondigitization workflowDriver behaviordemosaicingDeepFake Detectiondrone-projectordiffuse reflectionDOMINANT WAVELENGTHDECONVOLUTIONDiscriminant analysisDESCRIPTORDECEPTIONDISCUSSIONdefect detectionDBSDigital forensicDisparity mapdata visualizationdigital printingDetectionDynamic RangeDISTORTION-LIMITED SENDERDIGITAL ARCHIVEdisplaysDOMAIN-SPECIFIC FEATURE EXTRACTIONDutch 17th century paintingsDEPTH MAPdocument classificationdemosaicDispersed-dotde-fencingDigital CDSdigital objectsDifference scalingdisplay calibrationdeutanDCTdeblockersDRAWINGdigital color halftoningDirectional visibilityDISTANCE METRICDepth Image-based RenderingData collectionDairy managementDistortiondepth cameraDICHROMATIC REFLECTIONDomain Randomizationdecision makingdodecenyl succinic anhydrideDEPTH ORDERINGDepth mapDisplaysDEPTH UPSCALINGdefocusDepth cameraDIAMOND SEARCHDISPARITY SEARCH RANGEDataset imbalanceDecision Models in Artificial Intelligencedigital preservationDesigndrawings: multi-spectral imagingdrop speeddimensional accuracydigitisationDEPTH RECONSTRUCTION RANGEDenoising expedienceDIGITAL ASSETDIGITALIZATIONDISPLAY SYSTEMDUST DETECTIONDataset preparationdigital fabricationdocument securityDONALDSON MATRIXDISPARITY MAPDIGITAL CAMERADeepfake Detection EvaluationDEMOSAICKINGdynamic feature accumulationDRDeep convolutional neural networksDICOM
E 
ELECTROENCEPHALOGRAMEdge deviceESTIMATIONElastic-YOLOEmbedded VisionEYE TRACKINGELECTRON BEAM DETECTOREarly splitembedded informationESTIMATEEducationEMBEDDED INFORMATIONergonomicsEDGE-AWAREEMOTION DISTRIBUTIONEYE MOVEMENTEducation systemERPEXPECTATION-MAXIMIZATION (EM) ALGORITHMEXTRACTING IMAGES FROM POINTCLOUDSENHANCEMENTEncoder Decoder NetworkEye Blinking BehaviorEMBEDDED SYSTEMSextended realityexpressionEDGE ENHANCEMENTECCEMOTION PREDICTIONExtended Kalman FilterEnvironmentEthanol-water mixture dropletELECTRONIC DEVICE AUTHENTICATIONeducation analytics data visualization curriculum analysisEXPOSURE TIMEElectric vitrineEMBEDDED DEVICEEncrypted Traffic AnalysisEDGE DETECTIONEarth observation dataEdge detectorEXPLORATORY IMAGE SEARCHEnergy harvestingeye-tracking based 3D displayEVENT DETECTIONELECTROPHOTOGRAPHIC PRINTERExposureEnsemble learningEdge ComputingEARLY TERMINATIONemissionEulerian Video MagnificationEnhancementENDOSCOPYEMOTION TRANSFORMATIONEMOTIONexperimental resultsEnd-to-End Learningester acetal polymerEnvironment Recreationedge contrast sensitivityETHICAL HACKINGEuler video magnificationEXTRAPOLATIONevaluationExploration behaviorethical hackingeye tracking for AR HUDEfficiency improvementEMEEMERGENCY EVACUATIONEvent-based Vision SensorEXIST databaseeye movementEfficient Neural NetworksEmergency ManagementEVALUATIONEgocentric ImageENCRYPTED DOMAINEnsembleenergy harvestingEquiangular cubemapEmbeddedEXPERT VISUAL ASSESSMENTEMBEDDED VISIONedge detectionEMERGENT AUGMENTED REALITY PLATFORMSendmember extractionEDUCATIONElectrophotographic processEHEALTH APPEnsemble ClassificationEHEALTH DATA PROTECTIONEIGEN ANALYSISEnd-to-EndEnd-to-end simulationEvent-based Vision SensingEdge-preserving total variationElectron hologramExploratory VisualizationelastomerEEG dataEye tracking applicationsEnhancement algorithmsexif toolevent-based vision sensorelectrochromicEDGE POINT ICPEvent RepurposingEMVA 1288Evolutionary AlgorithmsEDGE-DIRECTED INTERPOLATIONEffective ResolutionEfficiencyEMANTING RAYSEye-trackingempirical studiesEvaluationEFFECTIVE COLOR RENDERING AND TEMPERATUREEdge computingEdge ProcessorsEye TrackingEMOJIEXTREME VISCOSITYEvent cameraedge mapenvironment visualizationEncodingEvent-based Visione-paperELECTRON-TRANSPORTING LAYERempirical detectorEXIFEndoscopic imagesEfficientNet recognition modelEPI analysisECGElectronic First Curtain Shutteredge-based spatial frequency responseevent cameraEHEALTH ANDROID APPSedge preservationEmpathy Buildingevaluation systemEdge artifactsease of useEvent SensingEDGEELECTROSPRAYINGemergent augmented reality platformselectric carError back-propagationEye trackingEMVAEnd-to-End Optimizatione-SFREnd-to-end performanceElectronic ShutterEEGeye movementsEXPERTISEELECTROKINETICSEquator biasECOLOGICAL TESTINGEnhancement of viewing angleexportEVENT RECOGNITIONEvent communicationExplainable AIExperiential LearningEstimation of resamplingError diffusionESP32-CAMelectro-opticemotionElectron tomographyExit pupilERROR DIFFUSIONEvaluation metricsEuclidean Colour SpaceegocenterEvaluation of whiteboard image qualityenergy distributionENVIRONMENTAL SUSTAINABILITYEmbedded SystemsEfficient deep learningEarly Modern Paintingsedaend-to-endEidetic recognitionEnvironment monitoringELDERLY USERSestimationExploratory data visualization and analysiserror diffusionExposure Bracketing StrategyEcologically-validelectronic imagingemulationemergency evacuationedge-direction featureExhibitionentropyEncoded phase maskEmotion RecongnitionEye MovementsECLIPSE SAFETYEXPERIMENTAL PRINTINGerror diffusion mapExtended RealityEPIPOLAR GEOMETRYEnd-to-end Systemeffect pigmentseHealthEYEEmbedded ProcessorsEDGE-SHARPNESS MISMATCHe-recordsEXPERIMENTAL PHENOMENOLOGYERROR CONTROLEmergent Augmented Reality PlatformsEye detectionExplainable Artificial Intelligenceedge computingEXPLOSIVE DETECTIONENRICHMENTEHEALTHentropy codingEIDOLON FACTORIESeye trackerelectronic machine readable travel documentsEMOTION EVALUATIONEYE MOVEMENTSedge artefactEdge DetectionEYE TRACKERENERGY AUDITENSEMBLEEccentricityEpipolar plane image
F 
facesFeature selectionFLUID SIMULATIONfilmfeature fusionFull-well capacityfirewallFace RecognitionFrost filterFiducial feature detectionfull body measurementFull reference image quality assessmentforensicsFemoral fractureforeground detectionFWHMFREE FORM MIRRORFiltering and denoisingfavorabilityFACEBOOK SURROUND 360FAST TRANSIENTSFringe Projection ProfilometryFacial landmark detectionFOCAL LENGTH TUNABLE LENSFloods detectionFAIR dataFADGIforwardFire detectionFUNDAMENTAL VISIONfish-eye cameraFALSE-COLOR COMPOSITESface priorityFOURIER SPECTRUMFAST FOURIER TRANSFROMSFresnel Phase PlateFoodfashion imagesFPFHFactoryFACIAL SHAPEFree ViewingFood-Borne ContaminantsFrame rate conversionFreespace detectionFingerprintFlarefMRIFake newsFacial pore warpingFinishingfatigue analysisFaster R-CNNfirmware analysisFREEDOM FROM INTERFERENCEFeature ExtractionFace MaskingFUSION ALGORITHMSfast inter codingFurniture-of-interestFourier PtychographyFADGI WORKFLOW STANDARDS DIGITIZATIONfixational eye movementsfluorescence synthesisFILE CARVINGFREE-SPACE SEGMENTATIONfilm restorationFLOW PATHSFISHER VECTORFourierFoca lengthforensic educationfourier ptychographic imagingfine artFood SafetyFuture trends in imaging technologiesfractal analysisfiltering and denoisingField of Light Display (FoLD)Fashion ImageFIXED POINTfacial landmarkFirearmfeature selectionflickerfloss, free, libre, open source softwareFEATURE RANKINGFace alignmentFrequency-domain analysisFine-tuningFacial Action AnalysisFast correcting while scanningFACE POSE ESTIMATIONFilm grain noiseFLUORESCENTFreeSpaceFusionFPSFunctional lightingFocal AccommodationFilteringFOURSEEFiltersFundamental of imaging and modeling of image formation,Optical imaging systems and lensesFluorescencefull-reference metricsFireballsFiltering and Denoisingfashion aestheticFlash Photographyforensic trainingFULL-REFERENCE METRICSFACE LANDMARK DETECTIONfacial expression recognitionFactor Graph-based Stereo Matching AlgorithmFLUORESCENT OBJECTSfisheye lensFixmatchFeaturesfractional non-linear contrast stretchingFlare measurementFacial recognitionFabricface learningfiber-reinforced polymerFERROMAGNETICFRACTALfull-parallaxfocal colorFORWARD SEARCHFace ForgeryFAKE VS REAL IMAGEFacebookFalsified mediaFull-reference Image Quality AssessmentFood safetyfacial recognitionFORENSICSFirst ResponseFRBRfashion photographyFIXED-PATTERN NOISEFew shot learningfiducial markersFIELD ROBOTICSFace DetectionfeaturesFAR-INFRAREDForest fire detectionfacial emotion imagefacial image processingFLOW VISUALIZATIONFILTER BANKfabricationFLOWFood Image ClassificationFEATURE SELECTIONFACE SPOOFING DETECTIONfeature pyramidfresnel zone plateFARM SIMULATIONFocal Plane ShutterForestryFood Image GenerationField of viewFusion Algorithmsflare lightfilm compsitingFULL HD|INTERMEDIATE IMAGEFILM PRODUCTION PIPELINEFLAREFEATURE FUSIONFootballFisheye lensFlood predictionforeground extractionFisheye cameraFULL-REFERENCEFlicker indexFluid dynamicsflicker photometryFundamental visionFOGRAField roboticsfluidfundamental vision, perception, cognition researchFabricationFOURIER OPTICSFaster RCNNFacial imagesforestFAST MOTION-SEARCHFeatureForeground detectionFundamental vision, perception, cognition researchflare testingFew Shot LearningFULL-COLOR 3D PRINTINGFIBER TRACKINGFloorplan generationFAST FOURIER TRANSFORMFixationFLYING EXPERIENCEFeature FusionFracture predictionFruit freshnessFULLY CONVOLUTIONAL NETWORKSfield roboticsFluorescent objectsFMRIFluorescence quantificationFood and Computer VisionFace detectionFalse colorFLUX TRANSFER MATRIXFluid controlFILTERING AND DENOISINGForgery DetectionFull-parallaxfeature learningfiltersFish freshnessFOREGROUND SEGMENTATIONFOCUS TOPIC: NOVEL TECHNIQUES FOR PROBING VISIONforgery detectionfactory automationfilm digitizationFACIAL LANDMARK DETECTIONfacial landmark localizationFerromagneticFault tolerant architectureForensicsFACIAL SKIN COLORFORGERY DETECTIONFace swappingFull-colorFEATURE EXTRACTIONFacial ExpressionsFilm fadingfilteringFocusing Effectfield-of-viewFast data retrievalFINGERTIP DETECTIONFeature vectorFeatures analysisFacial landmarkFixation patternFILTER DESIGNFake imagesfirmware vulnerabilitiesface recognitionFixed Pattern Noiseface morphingfuzzy-based convolutional neural networksFLUORESCENCE MICROSCOPYfisheyeFILTER KERNEL ESTIMATIONFLASHOVER PREDICTIONface pose normalizationFULL FRAME CCD IMAGE SENSORFOCUS MEASUREFusion algorithmsFovealFloating Diffusionfinite element simulationForensic Process ModelsFISHER INFORMATIONface perception in the blindFlicker measurementfull-reference image visual quality assessmentFACIAL COLOUR APPEARANCEFOVEATED JUST-NOTICEABLE-DIFFERENCE (FJND)functional safetyFrameFOOTBALLFacial Video InpaintingFUZZY SYSTEMFlicker SensitivityFace expression analysisFASHION MARKETFUNCTIONAL SAFETYFalling rocksFrequency of Correct Resolution (FCR)FPGAface detectionfirst line inspectionfrequency interpolationFeature de-noisingFood palatabilityFACIAL ATTRACTIVENESSfabric image preferenceFEEDFORWARD CONTROLfigure-groundfeature pyramid networkFAST ALGORITHMFully Convolutional NetworkFacial pore segmentationfacial appearanceFringe AnalysisFILTER SELECTIONfull-reference image visual quality metricsFace recognitionfixed aspect ratiofiber detectionface alignmentfused lassoFASHION IMAGINGFace trackingFirst-order image statisticsFeature extractionfiner-scale networkFAILSAFEFourier opticsFIXED PATTERN NOISEfour parallaxesFarnsworth-Munsell 100 hue testFDM color 3D printingFAST COMPUTATIONAL IMAGINGfloating focusFoveated RenderingFISHER VECTORSFundamental of imaging and modeling of image formationFlicker perceptionFIRST-PERSON VIDEOSFRANGI FILTERface trackingFourier FilterFisheye CameraFlickerfatigueFringe analysisFAST 2-D QUATERNION FOURIER TRANSFORMFELS INDICATORSfusion algorithmsFused deposition modelling (FDM)FOVEAL & PERIPHERAL VISIONFace maskFood DetectionFilter DesignFinBERTFEATURE COMBINATIONfast robust correlationForensic ScienceFull-parallax 3D displayFEATURES FUSIONfake passport photosFORENSIC CHALLENGESFPGA-SOCFire-tubeFace detection and face recognitionFACE RECOGNITIONfeature extractionFacial Expression AnalysisFace detection and recognitionFACE ALIGNMENTFood qualityFISHER'S METHODface simulationFOVEATED IMAGINGFABRICATIONFAST RADIO BURSTFace AnalysisFingerprintingfinite state machine
G 
GAZE RESPONSEgraphic artsgame designGAMUT BOUNDARYGAZE-CONTIGENT DISPLAYGenerative AIGAUSSIAN FILTERSGlobal shuttergraininessGuitar Teaching SystemgamesGAMUT MAPPINGGAMMA CORRECTIONglossGlobal motion vectorsGOODE HOMOLOSINE PROJECTIONGuestureGolden ConvertGlossGPU COMPUTINGGABOR Filtersgenetic algorithmGPU-accelerated algorithmguided image filteringGraph Neural Network (GNN)grayscale experimentglare in illusionsGAUSSIAN BLURGraph theorygroup lassogame engineGAMMA-RAYS CAMERAGRAYGradient Based AttacksGaze Analysis TechniquesGRAPH THEORYghost-paintingsgray-level co-occurrence matrixgamutGAZE PATTERNSGANsGRAININESSGRAPHENEGLARE DETECTIONgloss predictionGeometric CalibrationGAMUT FACEGamutGolf swingGEOMETRIC DISTORTIONSGamut mappingGLOSSGAZE DISRUPTIONSGame-based LearningGeneratorghostpaintingsGONIOMETERGlossinessGraphene InksGlobal processingGenerative Adversarial NetworkgyroscopeGeometric featureGamut problemGenetic algorithmsGRAPH VISUALIZATIONGRAPH CUTSGLOBAL MAXIMUM PEAKgraph matchingGraphicsgreen screenGLOBAL SHUTTERGAMUT VERTEXgridded dataGraph Representation LearningGREY-LEVEL CO-OCCURRENCE MATRIXGradient domainGRAPH SAMPLINGGRAPH CUTGenarative adversarial networkGenerative adversarial networksGenerative Adversarial Networks (GAN)GREEN ALGAEgenerative designGoogLeNetGAMMA-RAYSGAUSSIAN MIXTURE MODELGRIN lensesGROUND-TRUTH BASED VALIDATIONGestalt principlesGaze Contingent Displaygloss characterizationgloss perceptionGlobal registrationGREETING CARDSGAME DESIGN AND MECHANICSGMPHD filterGEOMETRIC CAMERA CALIBRATIONGuided image filterGeneralized Adversarial Networkgonio-spectral imagingGOAL DETECTIONGaminggamut volumeGamut MappingGONIOAPPARENCYGUROBI OPTIMIZATION FRAMEWORKGREEDY OPTIMIZATIONGrayscalegraffitiglasses-free 3D displayGlobal OptimizationGENOMICSgelatinGPGPUGlass Corrosiongeometric distortionsGREEN PLATE-MAKING TECHNOLOGYGPU ACCELERATIONGlare spread functiongloss measurementGUIDESguar gumGaze EstimationGENOTYPE-PHENOTYPE MAPguide rollerGEOMETRIC INTEGRATIONGEOGRAPHIC INFORMATION SYSTEMgeneration dependenceGStreamergaze trackingGeometric Correction EngineGENEALOGIESGPUGUIDE IMAGE FILTERINGGraph FusionGeneral ConsumerGENERIC FOURIER DESCRIPTORGLOSS PERCEPTIONGames for HealthGraynessghostinggray world assumptionGRAPHIC ARTSGRAPH DRAWINGGloss unevennessgoodness of model fitGaussian Distributiongeometric featuresGenerative Adversarial NetworksGENERATIVE ADVERSARIAL NETWORKghost paintingGame DevelopmentGame DesignGlasses-free 3D displayGradient Based SegmentationGANG GRAFFITI COMPONENT CLASSIFICATIONGLOSS MEASUREMENTGazeGRAVURE PRINTINGGRADIENT DOMAINGRAPH PROPERTIESgenerative adversarial networkGRAPHICAL PROCESSING UNITGISGLOBAL MEAN VALUEGrey relational analysisgraphical targetsGLOBAL DESCRIPTORSGoogle DaydreamGRAPH HIERARCHYGENETIC ALGORITHMglobal depth-mapgreedygeneral adversarial neural networkGabor filterGLOSSINESSgoniometrygood dataGhent AltarpieceGAINgrid viewgeometric meanGUITAR FINGERINGGRAY WORLD ASSUMPTIONgloss meterGRASPING PARAMETERGAN image detectionGRAY BALANCEGamut boundary descriptionGaussian Mixture models (GMM)GRID ALIGNMENTGAMUT VOLUME ETCgeneral adversarial networksGENERATION COPYINGGap StatisticGOOGLENETgradient operatorsGunshot DetectionGeneralizationGANgRPCGamma CurveGlaregenerative models
H 
HDR displayHIGH FRAME RATEHigh Dynamic RangeHDR DOWN CONVERSIONHDR (High Dynamic Range)HIGH QUALITYHeterogeneous ComputingHuman factorsHuman 3D perceptionhair toneHough transformHands-free InteractionHand pose estimationhighlight preservingHOLOGRAPHIC DISPLAYhuman visual systemHUMAN-COMPUTER INTERACTIONHALFTONE IMAGE REPRODUCTIONhalo effectHUE CIRCLEHISTOGRAM SPECIFICATIONH.264Hybrid HashHyperspectral ImagingHIVE cylinder displayHUMAN VISION MODELINGHDR VIDEOHybrid diffractive opticsHYPERBOLIC WEDGEHDR displayshermeneuticsHigh Performance ComputingHUMANITIES APPLICATIONSHyperspectral reconstructionHAND-EYE CALIBRATIONh-index Comparisonhuman-computer interfaceHERITAGEheritage sciencehigh dynamic range imaginghistorical document binarizationHebraicaHamming DistanceHue-preserving image processingHead-mounted Displayhigh-speed imaginghigh-resolution imagingHDR COMFORTHIGH DYNAMIC RANGE IMAGEHololensHYBRID SCREENhigh capacityhealthcareHIGH DYNAMIC RANGE (HDR)HUMAN STATE ASSESSMENTHDR COLORIMETRYHUMAN VISION ABSTRACTIONhigh dynamic rangeHPC clusterHistogram EqualizationHUMAN CREATIVITYHyperspectral imageshuman visual perceptionHead-mounted eye tracking technologyHYPERSPECTRAL IMAGINGHEAD-MOUNTED DISPLAYHUMAN PERCEPTIONHead TrackingH264HIERARCHICAL ANALYSISHandwritingsHTC Vive ProHIGHER-ORDER SINGULAR VALUE DECOMPOSITIONHDR IMAGEHALFTONINGHue shiftHighway pilotHuman FactorsHealthcare SkillsHuman visual systemHigh-qualityhuman visionHighlightsHuman Visual SystemHomeland SecurityHyperspectral imagingHOG FEATUREShuman factorshalftone level selectionhazeHRholefillingHigh dynamic rangeHelmholtz-Kohlrauch EffectHOGHIGH-SPEED VIDEOHIERARCHICAL STRUCTURESHUMAN VISUAL SYSTEM MODELHARDWARE ADAPTIONHash tablesHEVC IMPROVEMENTSHUMAN-HUMAN COMMUNICATION DYNAMICShelmholtz-kohlrauschHuman-Subjects Quantitative StudieshololensHISTORICAL ARCHIVE OF THE EUROPEAN COMMISSIONhistogram of oriented gradientHuman-machine InterfacesHalo effectHuman-computer InteractionHealth informaticshorizontalityHuman Visual PerceptionHALLUCINATIONholographyhybrid collaborationhistorical inksHAND POSE ESTIMATIONHaralick featuresHealth sensorHistoryHIGH DYNAMIC RANGE IMAGINGHalftoningHUMAN COLOR VISIONH.264/H.265 encoding & decodingHigh-Dynamic Range (HDR) and 3D imagingHYBRID DICTIONARY LEARNINGHigh-Dynamic-Rangehazmat label detection and recognitionHeads-Up DisplayHolistic image manipulation detectionHazeHYBRID LOG-GAMMAHMD VS IMMERSIVE VRHUMAN MACHINE INTERACTIONHUMAN PERFORMANCEhue mixtureHead-Mounted DisplayHair colorHUMAN DETECTIONhuman computer interfaceHDR contentsHistorical ParchmentHUMAN COLOR PERCEPTIONHigh Saturationhigh completenessHyperspectral microscopeHIGHLIGHT DETECTIONHorizontal band noisehyperspectral imagingHexapod Robothandshake measurementHigh speedHISTORICAL CHINESEHandwriting AnalysishdrHilbert curvehead-mounted displaysHuman visionHOT PIXEL DEVELOPMENTHuman DetectionHuman ParsingHYPERSPECTRALHyperspectral Visionhuman skin chromophoresHIGH DYNAMIC RANGEHAT MATRIXHardware ready bitsHyperspectral visionHomographyHUMAN VISUAL SYSTEMHigh-resolution projector compensationHeterogeneous SoCsHoney Bee DetectionHuman Body Measuring Toolhigh speed sinteringHSHHEVCHardware-In-the Loop imagingHUMAN POSE ESTIMATIONHALFTONEHue appearanceHAPTICSHigh dynamic range imaginghuman-machine interactionHAND GESTURE RECOGNITIONhistorical manuscriptHISTOGRAMHead-mounted eye tracking data analysishistoryHueHISTORIC PHOTOGRAPHSHierarchical modelhot pixel developmentHDR color spaceHunt EffectHybrid Log-Gamma (HLG)High Sensitivityhuman eye modelHigh-dimensional visualizationhyperspectral imagesHemispherical harmonicsHDR Tone mappingHeart rateHead-up displayHandwriting RecognitionHEALTHCARE INFORMATION SYSTEMSHelmetHealthcare AIHYPERSPECTRAL IMAGEHevcHelmholtz-Kohlrausch effectHIGH PRESSURE DIE CASTINGHAPTIC DEVICEHVSHUE TRANSFORMhierarchical microcrystalsHAIRINESS OF KNITTED FABRICSHDR (HIGH DYNAMIC RANGE) IMAGINGHIGH-RESOLUTION STYLEhigh viscous jettingHuman perceptionHistogramhead mounted displaysHUDHAND RADIOGRAPHH.265human perceptionHead-based PointingHEART RATEHybrid EVS+CIS sensorHDR laboratory setupHIGH-PRECISION 3D SENSINGheuristichigh dynamic range (HDR)Holstein cattlehealthcare securityHUEHexa Deca BayerHigh-dimensional low sample sizehapticshistorical document processinghigh sensitivityHTTP-based adaptive streaminghead-mounted displays (HMDs)Hand hygieneHigh Dynamic Range (HDR)Holographic DisplaysHANSHUMAN VISIONHEAD-UP DISPLAYH.264 COMPRESSIONHUMAN BEHAVIORHMDHierarchical Task NetworkHANDEDNESS SWITCHHigher-order neworkHigh conversion gainHEAD DETECTIONHough Lines DetectionHyperspectral databaseHidden Markov modelHigh-Performancehomeland securityHORN-SCHUNCKhalftone image optimizationhardness testinghighly saturated illuminanthighlighter mark featuresHigher-order tensorHIGH THROUGHPUThandshake profileHDRhumanHYPERSPECTRAL FUSIONhalftoneheat supplyhyperparameterHYPERSPECTRAL IMAGEShigh resolution panoramaHTNHUMAN VISUAL SYSTEM MODELINGH.265 EncoderhalftoningHUMAN SKIN APPEARANCEHalftoneHigh dynamic range (HDR)human placentahuman behaviorHUMAN VISUAL PERCEPTIONHuman Visionhistoric dataHapticheterogeneous content visualizationhighlight detectionHUMAN FACTORShuman activity recognitionHANDS-ON EXPERIENCEHETEROGENEOUS PROGRAMMINGhead-mounted display
I 
INTERDISCIPLINARYIMAGING ALGORITHMSink droplet image processingimage reintegrationIMAGE QUALITYImaging System Measurementimage morphingINKJET PRINTINGIMAGE SYNTHESIZINGInkJet PrintingIMAGING PIPELINEilluminant color estimationIntegrating sphereINDOOR SCENE SEGMENTATIONindoor positioningIEEE P2020 Automotive Image Quality StandardsimageIMAGE FUSIONimmersive VRImage Sensorsindoor layout estimationImage DegradationINTEGRAL PHOTOGRAPHYINTERNET OF THINGSinkjet inkimaging algorithmsIMAGESimage processing, computer vision, and remote sensing in food and agriculture systems: farm, livestock, production, restaurantINTEGRATING SPHEREimage understandingInverse halftoningImage Quality Evaluation Metricsinstance segmentationImmersive and extended reality imagingIR sensitivityIMAGE FORENSICSimage scramblingImage Signal Processor Pipeline (ISP)image authenticationInkjet printoutImaging System OptimizationImage signal Processor (ISP)image smoothingIMAGE MODELINGiso standardsImage naturalnessIMAGE RECONSTRUCTIONImage signal processors (ISP)ICSImage retargetingintegra displayImage ForensicsICC PROFILEIMAGE REGISTRATIONIMAGE BASED MEASUREMENTSImage histogram matchingInverse RenderingimagingInterpretabilityintrinsic decompositionimmersive capture systemsimaging systemsInjection MoldingINDUSTRIAL PARTSIMAGE STATISTICSINTERACTIVE VISUALIZATIONSImage defect detectionIMAGE STITCHINGimage recognitionImage StabilizationINDOOR POSITIONINGINVERSE TONE MAPPINGIterative ExplorationImage ProcessingImmersive video 6DoFIntegrated photovoltaic cellsIMAGE EMOTIONilluminant estimationIMAGE OPTIMIZATIONImage reconstructionIMAGE MATCHINGimage-to-image translationISO speed ratingIMAGE QUALITY INDEXIMAGE RESTORATIONINTERNETImage information capacityimage synthesisIndoor floorplan generationIEEE P2020Image analysis systemIndustrial Internet of Thingsimage segmentationINTERACTIVE SEGMENTATIONImage featuresimage-based gloss meterInteractiveImage UnderstandingIMAGE RECOVERYimage visual quality assessmentImage synthesisINFRASTRUCTURE MAINTENANCEintegrityimage manipulationIdeal Observer ApproximationIMAGE ANALYSISImage Recognitionimage normalizationimage fusionIMAGE ANALYTICSIMPROVISATIONinverse problemsINKJETinterference photographyITERATIVE CLOSEST POINTSIMAGE CODINGIInstant Messaging Services (IMs)IMAGE-BASED MEASUREMENTSimage denoisingimage classificationIMAGE MASH-UP AND RE-MIXINGINTERACTIVE MESSAGING APPLICATIONInfrared ImageryIMAGE DENOISINGImaging DeblurringImage CompressionImage quality matricesImage SegmentationIMAGE CONTENTINTER-OBSERVER DIFFERENCESimage reconstructionIMAGING STANDARDSimage transformISPInline Inspectionin-house appINTERPOLATIONimaging analysisImage Quality (IQ) metricsITERINTRODUCTION: BRIEF HISTORICAL NOTESImage IntegrityIMAGE ENHANCEMENTISOSURFACEImage qualityIntersection Topologyinformation capacityIEEE-P2020IMAGE SENSORImage splicing localizationIndoor stereo SLAMImmersive ImagingINTELLIGENT ROBOTSinertial sensorsilluminant correctionIMMERSIVE VIRTUAL REALITYImage quality metricIMAGE SHARPENINGImage Systems SimulationIoT Securityimage quality datasetImage RobustnessIMAGING COMPUTATION WITH PHYSICAL DEVICESimager defect detectionInverse Problemsimage sensorsindustrial control systemsImage quality evaluationimperial portraitureinformation compressionImage information metricINPUT DEVICE TRANSFORMIterative reconstructionImage processingITERATIVE CLOSEST POINTIMAGE PROCESSINGIntegrated Surrounding SurveillanceImmersive mediaIMAGE AND VIDEO COMPRESSIONInternshipsIMAGE AND VIDEO ANALYSISIndustrial Defect SegmentationINTERDISCIPLINARITYIMAGE SYNTHESISIMAGE RETRIEVALInstance Segmentationimage debandingillumination conditionImpression factorImage-Based CompressionIMAGE-BASED LIGHTINGImage Synthesisimage forgeryinkjetISO19567IMAGE VISUAL QUALITY ASSESSMENTImage sensorImage TexturesIoT securityINSTANT MESSAGINGImage Quality MetricsINTERIMAGING APPLICATIONSImage DespecklingImage fusionink recipesimage matchimage-based renderingimage registrationImage Quality Assessmentin-cabin imaginginpaintingINFORMATIONILLUMINANCE LEVELSIndoor decorationInteraction architectureIMAGINGimage quality analysisInline inspectionImage ResolutionIMAGE INTERPRETATION BY MACHINESiOSImage RecoveryISO12233IMAGEIRREGULARinternet securityIMAGE PYRAMIDImmersive experienceIMMERSIVE MULTIMEDIAImage reproductionimage forensicsIridescenceImage noiseInkjet printerIndex Terms — Electrophoretic display (EPD)INFORMATION HIDINGimage degradationISO 20462-3:2012Image ForesnsicsImage signal processorintrinsic imagesImmersive Projection TechnologyImage-Based Measurementsimage compressionImage tamperingImage systems simulationIMAGE STRUCTUREISO20490image analysisiToFindoor air qualityIMAGERIMAGE FORENSICS APPLICATIONImitation Learningillumination estimationImmersive Capture Systemsimage statisticsIATimage stabilizationImage systems engineeringImage prossesingImage Signal Processor (ISP)image signal processor (ISP)IMMERSIVE METHODOLOGYImage denoisingINDOOR MAPPINGimage learningINK-JET PRINTINGINK JETInter-species communicationImage Quality MetricImage Transfer TechniqueIMMERSIVE FOOTBALL EXPERIENCESIMAGING CONDITION CORRECTIONInternet of thingsInterpolationintelligent robotsImaging SystemImage color extractionINK SAVINGILLUMINANT ESTIMATIONIntegral imaging systemINTRODUCTIONINTERACTION SYSTEMSILLUMINATION ESTIMATIONinline inspectionIMMERSIVE ANALYTICSICTCP color representationISO15781ink jetideal observerImage sensorsImage-based Compressioninverse imagingImage quality AssessmentIMAGE COMPRESSIONImage classificationImage sensor characterizationInformation CapacityITERATIVE RECONSTRUCTIONImmersive experimental methodologiesIMAGE SEGMENTATIONImaging for scientific applicationsimpressionsINTELLIGENT VEHICLESinkIMAGE EQUALIZATIONImage ClassificationITS4S DatasetinterreflectionsIntegral imaging displayimage structureimage saliencyInformation Visualisationill-performing classesInformation VisualizationInkjet PrinterINTERNAL VISUAL NOISEISO 15739infrared-filter imagesImage quality metricsIntegral photographyIMAGE UNDERSTANDINGIMMERSIVE DISPLAY SYSTEMSimage editingINTERFACEImage CodingIMAGE UTILITY ASSESSMENTimage RAWINTERMEDIATE IMAGEImage-based dietary assessmentilluminationImage attributionINTRA PREDICTIONIMAGE GRADIENTSImage EnhancementImage analyticsIMAGE ROBUSTNESS AND NATURALNESSIntegrity verificationIllumination invarianceImprovement the color appearanceINTERACTIVITYIIIFImage scrambleimage resolutionIoTimage enhancementillumination modelIMAGE QUALITY METRICISO 16505ISO 12233image copy-move forgeryImage segmentationIMPREGNATION PROCESSINK-USEImaging SystemsImage QuiltingIntegral displaysImage LabelingImage DeblurringIT securityIntegral PhotographyIMMERSIVE IMAGINGIndependent Component Analysis (ICA)intelligent surveillanceImage retrievalImaging sensorILLUMINATION VARIANCEIMAGE QUALITY ENHANCEMENTIMAGE QUALITY MEASUREInpaintingIPimage processingIndexImage denoising networkIMAGE CONTENT ANALYSISimage sensorIMAGE ENCRYPTIONIMAGE IMPROVEMENTImage QualityImage-based degradationsIMAGE MANIPULATIONIN-PAINTINGIMAGE SENSORSinkjet printerImage forensicsIMAGE EDITINGImage MattingIMAGE CLASSIFICATIONILLLUMINATION ESTIMATIONIndoor Stereo SLAMILLUMINATION AND REFLECTANCE SPECTRA SEPARATION (IRSS)image cuesIMAGE DEBLURRINGImmersive ExperiencesILLUSTRATIONimage aesthetic assessmentInverse GraphicsIncident CommandingILLUMINANT COLOR ESTIMATIONimage matchingimage viewerImage Quality RulerInnovationImagingICtCpInkjet printingINTEGRAL 3D DISPLAYInksilluminated manuscriptImage ReconstructionInternational Collaborationindustrial inspectioninkjet printingImage quantizationImage compressionIR imagesINPUT DEVICE TRANSFORMSIMAGE QUALITY EVALUATIONIMAGE CLUSTERINGIMAGE DEHAZINGIntelligent RobotsIMAGE QUALITY ASSESSMENTimage quality metricINTENSITY INHOMOGENEITYink-jet print headsillumination invarianceINFRAREDInstrument panelsinteractive mediaimage preprocessingIMAGE SIGNAL PROCESSING PIPELINEipRGCIMAGE SIGNAL PROCESSINGISO27001Illuminationimage forensic analysisIdentity VerificationIndustrial Defect DetectioniPhoneImage Steganographyimmersive ARImaging Algorithmsinformation systemsimage captureimage sharpeningIMAGE ANALYST EXPLOITATIONIMAGE DATABASEintraocular scatterideal obseverImage signal Processorimage quality assessmentimmersive mediaimage restorationIIoTIllumination Scenariosilluminant invarianceImage Signal ProcessorInk-jet Printed Dopant LayerISO 12233 standardImmersive Design EngineeringImmersive Analyticsimaging modelImage SensorICCImage encryptioninternetimaging software ease-of-use practical free open sourceIll-posed problemink systemimage processing historyIntelligent robotsimage permanenceImage Processing immersive cultural heritageInverse imagingimage gradientsImpulse Radio Ultra Wide BandImage quality rulerInkjet PrintingImage categorizationImage SubtractionImage verificationINTERFEROMETERInvertible embeddingICPIMAGE ARTIFACT DETECTIONImplicit FunctionIQAIntegrated PlatformImage-based Dietary AssessmentINTERIOR DESIGNImage Quality EvaluationImage Restorationimage flickerImage alignmentISO 12233 ResolutionIntegrationIndustrial inspectionIOTInteractionImage simulationINTERFERENCEINK-JET TEXTILE PRINTINGInternet of Thingsinformation technologyImage Noise ReconstructionIMAGER DEFECT DETECTIONIMAGE FORMATION PROCESSINDUSTRIAL INSPECTIONIndoor localizationIMAGING SYSTEMSImage InpaintingImage Analysisimage distortionIterative AlgorithmInternal ReflectanceIMAGE CODECSIMAGE RESOLUTIONImage quality assessmentidentificationInteractive visualizationimbalanceImage Signal ProcessingInk-jet printingImmersiveinformation theoryImage stitchingInternet of Things edge imagingIterative Closest Point (ICP)Inspectionimage qualityInspection in harsh environmentsInverse functionImage steganographyIMAGE SYSTEMS SIMULATIONimage quality metricsINTER-REFLECTIONSintelligent monitoringimage crop wideningImage and Vision ProcessorsImage Registrationillumination correctionIndustrial InspectioninteroperabilityIdeal ObserverImage enhancementImagery PerceptionsImage forensics, Camera model identification, Source attribution, Convolutional neural network, Deep learningIDEAL OBSERVERinkjet printing banding defect compensationImage editingIntelligent Vehiclesimmersive imageryIndustrial defect detectionImage-Based Data InterfacesinfraredIMMERSIVE STEREOSCOPIC ENVIRONMENTSINVERTIBILITYImage aestheticsInterferometryInkjet inkInkjetIlluminant estimationIMMERSIVE PROJECTIONImplicit SurfaceIntelligence Cycle
J 
JOINT COLOR-NIR IMAGINGJPEG compressionJoint Attention for Autonomous Driving (JAAD)joint model-based and learning-based frameworkjoiningJohnson criteriaJPEG quality factor estimationJoint Camera and CV OptimizationJNDJPEG2000JPEG ADDITIONAL COMPRESSIONJOINT GEOMETRIC CALIBRATIONJPEG compression detectionJacinto PlatformjpegJPEG-XTJavaJoint design of diffractive optics and image processingJoint DistributionJUST NOTICEABLE DIFFERENCESJUST-NOTICEABLE-DIFFERENCEjust noticeable differenceJAB CodeJOINT IMAGE UP-SAMPLINGJPEGJPEG additional compressionJoint statistical image reconstructionJoint optimizationJOINT IMAGE DENOISING
K 
Kalman FilterKERNEL MAPSKinectKansei EngineeringKSM hue coordinatesKURTOSISkTC noiseKeypoint AlignmentKEYLOGGERKINESTHETIC HAPTIC FEEDBACKKUBELKA-MUNK MODELKINECTK-means algorithmK-means clusteringKALMAN FILTERSKEY POSE DETECTIONKNOWLEDGE SHARINGKNOWLEDGE-BASED TAXONOMIC SCHEMEkey management protocolKubelka-MunkKEYSTROKE LOGGERKen DomonKnot Theorykeyword8KNN AlgorithmKintsugi 3DknowledgeKPIKey performance index (KPI)keyword7K-meansKeyword detectionKernel-level rootkitKnowledge DistillationKOLMOGOROV-SMIRNOV TESTKnowledge distillationKEY FRAME EXTRACTIONKeyword Extractionkeyword6KNOWLEDGE DISCOVERYk-meanskeyword9Keystroke Biometrics
L 
LipLAPLACIAN EMBEDDINGLegged Locomotionlikelihood ratio testLATENCYLAYERED LIGHT FIELD DISPLAYLINEAR REGRESSIONLIGHT SCATTERINGLOGO RECOGNITIONLIGHT FIELD PROCESSING ARCHITECTURELED LUMINAIRESLDRLow depth noiseLocal MultiplayerLiDARLip analysisLUMINANCE RATIOLINEAR MAPPINGLaccollow noiseLDR-to-HDR image mappingLMTlook-up tableLIE GROUPSLSTM networkLow Light PerformanceLocalization Mapping & NavigationLinear inverse problemsLATEX INKLEAST-DISSIMILAR COLORlight field cameraLED LIGHTINGLight field renderingLIFETIME READINGlocal featuresLiDAR technologyLIDARLightweightLow-cost camera-projector systemLabelinglocal binary patternsLinear Discriminant Analysislung cancerLow read-noiseLIVENESS DETECTIONLow CostLight matchLong-Distance TestingLLMLINEARITYlow complexityLOCAL SPATIAL CONSISTENCYlinear regressionluminescent polymerLCDLABORATORY-SETUPLow-contrast ImagingLarge OLED DisplayLOUDLOW LIGHT CONDITIONLight colorLight fieldLow Optical Crosstalklightness contrastLOCAL BINARY PATTERN (LBP) OPERATORSLight field image acquisitionLong-wave infrared imageLED-basedLATERAL-ELECTRIC-FIELD CHARGE MODULATORLASER PROJECTORSLow-quality imageslaser scanninglightweightLatencylightnessLIGHT FIELD 3D DISPLAYlost artLinguisticsLaplacian pyramid of adversarial networksLBPLEARNINGLight field imaginglens distortion correctionlow exposure pixel gridluminancelooted excavationLED-based primariesLinearLow Rank Structured Matrix CompletionLow power CMOS Image Sensorlocal encryptionLighting visual aidLong Short-Term Memory (LSTM)landmark detectionLocal OptimizationLOCALLY LINEAR EMBEDDINGLight-field Display (LfD)Light scatteringLUMINANCELightfield capturelaser speckleLiDAR systemslarge color differencelightness algorithmsLee filterLuminanceLight presetLow-rank tensor completionLight field displaylaser printerLIQUID CRYSTAL DISPLAYLidar sensorsLocalizationLOCAL BINARY PATTERNSLGLIGHTNESSlight-fieldlidarLensless imagingLOFITreCLens PSFLight FieldLAGRANGIANLIVER DISEASELocal Binary PatternsLWIRLarge DatasetsLOCAL CONTRASTlightfastnessLONG SHORT-TERM MEMORYLight sourceLEGACY DISPLAYSLow LightLocal descriptorslight field visualizationlayered manufacturingLippmannLEAST ANGLE REGRESSIONLEDlicense plate detectionLight ray shiftingLOW-LEVEL VISIONLow cost hardwareLow visionLENS DISTORTIONLarge-format photographyLOW PASSlong distance jettingLate fusionLuminance Measurementslarge-scale dendrite coreslocal non-linear contrast stretchingLarge Language ModellateralizationLOCAL IMAGE CHARACTERISTICLow voltage 0.7μm pixelLaserJet PrintingLiDAR and camera fusionLa Condition HumaineLUCAS-KANADElegacy iot device interfaceLight capture and sensor technologieslcdLarge Foundational ModelsLarynxLINEAR DECODERlow-barrier to entryLMSLEARNING ENHANCEMENTLINE SEGMENTATIONLAGUERRE GAUSSIMAGE DECOMPOSITIONLeakage preventionlithium niobateLED Flickerlow frequency lightinglandslide detectionLabel spaceLow light enhancementLOCOMOTION TECHNIQUESLight Field DisplayLinear ClassifierLINE-BASED DETECTIONlight fieldLocal Color PatternLEGHlenticular lensLOGO DETECTIONLong short-term memoryLocal polynomial approximationLIGHT FIELDSLIGHT ADAPTATIONlight field reconstructionLarge Scale TrainingLive MusicLanguage learningluminous efficiencylikelihood ratioLED light sourcesLinear AcceleratorLOCAL DIRECTIONAL PATTERNSLOW MAGNIFICATION OPTICAL REPRODUCTIONLIBRARIESLearningLens flareLight field displaysLIVE BROADCASTLaser Quadratleaky-modeLIGHTFASTNESSLow density point cloudLIE ALGEBRASLip Reading DatasetsLaminographylightweight modellaserLight Field CodingLow VisionlightingLiDAR applicationsLinear patternLENS CHARACTERIZATIONlinked dataLighting AnalysisLIGHT FIELD RECTIFICATIONLOG POLAR TRANSFORMLighting communication functionLABELINGLINKED OPEN DATALOCAL BINARY PATTERNLane Modelling LCD display characterizationLAGLuminance MeterLENS ARRAYLIGHT FIELD CONVERSION PROCESSlighting analysisLost artlinear-path measurementLIGHT FIELDlosslesslight-field captureLocal Defect ClassificationLIGHTINGLOCK-IN PIXELLiquid crystal variable retarderLogarithmical Image Visualization Techniquelight fieldsLED BINNINGLITHOGRAPHYLOCK-IN DETECTIONLightness/Brightness ScaleLIQUID CRYSTAL LENSLocal processingLicense plateslightness perceptionLaplacian pyramidLight-field displaysLine extractionlight field retargetinglocalizationLight field compressionLidarLaplacian of GaussianLimited Angle X-Ray TomographyLearning analyticsLearned image compression methodsLEDsLOOP CLOSURE DETECTIONlbpLinear discriminant modelLibrarieslow-lightLOGARITHMIC TONE MAPPINGLOW ACCELERATION VOLTAGELeaf Shutterlow cost sensorsLAMBERTIAN MODELLe Blanc-SeingLIGHT EFFICIENCYLOCALIZATIONLED flickerLASERloop closure detectionLOGISTICline elementlow-light image enhancementLIGHTING REPRODUCTIONlightness illusionsLARGE-SCALELinked Open Usable DataLuther Conditionlow sidelobe level of spectrumlinear transform estimationLSTMLBP histogramlight absorbance measurementsLocal quality perceptionLASER CUTTINGLook Modification Transformlight field renderingLens Distortion Correctionlock-inLINE SCANNING
M 
MICRO-LED DISPLAYMANUFACTURINGMulti-ScaleMCMLmultispectral reconstructionMudmobile visualisationMotion BlurMicro LensMultimedia securityManipulation DetectionMOTION ESTIMATIONMass SpectroscopymagnetometermetadatamtfMachine Learning with hand-crafted and learned feature spacesMobile SystemMicro-expressionsmagnetic resonance imaging (MRI)MPEG-DASHMILVUSMaterial EstimationMaterial Classificationmultispectral pedestrian detectionMATERIAL PERCEPTIONmachine learningmotion learningmultimedia on mobile devicesmicro-gridMULTI-IMAGEMulti-image capture and rendering (e.g., NeRF)Multiview 3D displayMEDICAL IMAGEmeasurement scalesmu-factormonochromatic primariesMetadata managementMemory palaceMotion compensated frame interpolationMULTISPECTRAL DATA SETMovie character identificationMULTI-FRAME SUPER-RESOLUTIONmosaicMIDDLE LINEMultiple Granularity NetworkMAGE DETECTORMETADATA RETRIEVALMappingMNISTMelaninmultiview displaymultiscale saliency modelMaterial appereanceMULTISPECRAL IMAGINGMACHINE LEARNINGMODULAR HISTOGRAMMULTI-SENSOR IMAGINGMedia ForensicsModel-Based ImagingMODEL FITTINGMunsell color systemMETRICS ANALYSISMultivariate curve resolutionM-estimationMATERIAL TEXTUREMedian Threshold BitmapMULTI-LINE SCANNINGMULTISPECTRAL IMAGINGmel spectrogramsMASS DIGITISATIONModulation Transfer FunctionMUSCLE SPINDLEMulti-class vessel detectionMotion PlanningMammogramMultimedia forensicsMicroscopic imageMultiscale Salient Local Binary PatternsMOBILE IMAGINGmultispectral imagingMachine visionMOBILE DEVICESModel SurgeryMETHOD OF ADJUSTMENTMULTI-SPECTRAL SATELLITE IMAGESMOBILE WINDOW MEASUREMENTSMaterial recognitionMETHODSMixed Attention Cross Stage Partial (MACSP)Multimodal ImagingMINDMIPI cameraMueller Matrix ImagingMODULAR LENS CHARACTERIZATIONMONOCULAR SLAMMachine learningMATCHINGMEANINGFUL-ENGAGEMENTSMUSICMachine Visionmotion representationmobilitymicrofabricationMRI Model IdentificationMaterial captureMTF deconvolutionmaterial propertiesmaterial perceptionMemory coloursModulation transfer function (MTF)Model OptimizationMulti-shot Super-resolutionMonocular depth estimationMCP IMAGE INTENSIFIERMDSmodulation transfer functionManipulation detectionMEASURE OF IMAGE ENHANCEMENTmulti-userMobile Image SensorMULTI-COREMEDIA RELATIVE COLORIMETRYMaritime surveillanceMental stress estimationMatrix embeddingMRI SegmentationMobile cloud computingmode decisionMOBILEManuscript InvestigationManufacturing infrastructureMULTI-CAMERA SYSTEMSMulti-view imageMULTI-SPECTRAL IMAGINGMODELING CREATIVE PROCESSESMULTI-SCALE MATCHED FILTERMULTIMEDIA INDEXINGMOBILE HEALTHCARE SYSTEMSmirror arraymotion vectorMultitask Learningmass-mediaMassdigitizationMultichannel LED LightingMultimodal gesture controllerMultithreadingMueller matrix imagingmedia planningMODULATION TRANSFER FUNCTION (MTF)metricmagnetic polaron moleculemusic sourcesmobile forensicsMotion Processingmultisensory face perceptionMOBILE DOOR MEASUREMENTSmetric learningmulti-channel edge detectionMULTI-LEVEL MATRICESMalicious steganographyMaltegometricsMULTIMEDIA ANALYSISMULTIVIEW 3D DISPLAYmanuscriptsMultibit CMY halftonesMichelangeloMultimedia Forensicsmechatronicsmulti-view plus depthMEMORY COLORManual assemblymodulatormaterials scienceMotion compensationMSFAmaterials characterizationMotion VectorsMOTION ENCODERMEMORYmultichannel LED systemmicrofadingMODIFIED LIKELLIHOOD RATIOMobile Camera PhoneMRImicrolensMulti Light Image CollectionsMAXIMUM LIKELIHOOD ESTIMATIONMAXIMUM LIKELIHOOD DIFFERENCE SCALINGmulti-scale deep networkMAXIMALLY STABLE EXTREMAL REGIONMetrology of AppearanceMultipath effectmultimodal authenticationMULTI-TONINGMethod of lociMANIPULATION DETECTIONmulti-spectral imagingmaterial appearanceMirror arraymetrologyMULTI-TARGET TRACKINGMultispectral ImagesMeasurement systemmathematical morphologyMULTIPLE LIGHT SOURCESmedical imagesMutual illumination effectmobile healthcareMultiple directional lighting opticsMulti-Camera NetworkMODULAR FRAMEWORKMtF areaMUSEUMMechanical measurementsMonochromatic DecompositionMaxwell methodmedical applicatiomMedia Separationmedical image segmentationMobileNetV2multi-modalMulti-pedestrian tracking (MPT)Masked faceMorphological FillingMultimedia Securitymedian filterMULTIVIEW GEOMETRYmagnetostrictive printheadmultimedia analysisMask RCNNminimum entropy modelmobile phoneMeasurementMetameric coloursMarked Point ProcessmultispectralMP4metasurfacemultisensory perceptionmobile ImagingMULTI-LEVELMULTILAYER DISPLAYMultispectral imagesMOVEMENT DETECTIONMATERIAL REPRODUCTIONMP3, DRMMathematical Visualizationmultiple light sourcesMulti-sensor Data FusionMODEL BASED IMAGE RECONSTRUCTIONMETA-ALGORITHMICSmotion picture filmMulti-View DisplayMulti target trackingMULTIOBJECTIVE OPTIMIZATIONMobile phone camerasmultispectral sensormotionMid-air imagemulti-object trackingmultimodal large language modelsMTF50medical imagingMSB PREDICTIONModel comparisonMOBILE VIDEO PROCESSINGMULTI-ANGLE REFLECTION MEASUREMENTmappingMixed LightingMETAMERISMMUSCULAR ACTIVITYmaximum likelihood estimationMaterial decompositionMach bandsMicrofluidicsmemory colormobile devicesMetal artifact reductionmicroclimateModulation ClassificationMULTIPLE DISTORTIONSMULTI-IMAGINGmagnitude estimationMOBILE DEVICE SECURITYMEANING MAKINGMuzzlehead Detectionmicroscopymulti-channelmulti-camera systemmodelizationMultimedia AnalysisMULTI-LINE SCAN CAMERAMULTI-LINE SCAN IMAGINGMULTIPATH SIGNAL PROFILEMeasurement UncertaintyMulti-view codingmultimodalMetadataMultimediaMETAL ARTIFACTmultimediaMAPPINGMOBILE PHONESminimal assumptionMotion detectionMulti-pedestrian trackingMulti partial resetMobile 3D displaymulti-sensoryMixmatchMean-shiftmatte surface finishingMotion correctionmedical image processingmass serializationMachine LearingMULTIMEDIAMODIFIED LEAST ANGLE REGRESSIONmedical applicationMOTIONMirco-lens arrayMultispectral imagingMetrologymultitaskMobile phone cameramanufacturingMATERIAL CLASSIFICATIONmobile application developmentmulti-scale histogramMarkovmonitoringmicrofichemeasurementMethodologyMEAL ASSISTANT ROBOTMATRIXmotion blurmagic matrixMelanoma SegmentationMunsell huemultigrid optimizationMULTI-VIEW STEREO MATCHINGMucosal Wavemodel curriculumMicro-expression spottingMATHEMATICAL THEORY AND PHYSICAL MODELSMEDIAN REGULARIZATIONmulti-view displayMargin Skew Detectionmulti-view face alignmentMEDIA COLORmultispectral imageryMarginal lossmedia forensicsMotion searchModel-based ImagingMOTION PARALLAXMULTIPLE DISPLAYSMeteoritesmean opinion scoreMultimedia applicationsMicroscope 3D imagingMicrosoft HoloLensMulti-view RenderingMonk skin tone scalemicro gridmachine visionMEDIAmagickMatrix-RMODELINGModelingMICROSCOPYMain colorsMICROARCHITECTURAL ANALYSISMEDICAL IMAGINGmobile laboratoryMean co-located pixel differenceMultitask learningMethod DRAMOBILE SYSTEMmeasure of color image enhancementMQTTMENTAL ROTATIONmanual lensMTFMODELMedical image perceptionmaterialityMammogramsMODEL-BASED APPROACHMUSEUMSmeter readingMACHINE LEARNING TECHNIQUEMETRICSMedical imagingMachine LearningMAGNITUDE ESTIMATIONMini ReviewModel inference metricmultilevel phase mask designMASKING EFFECTmultiple projectorsMuseum tour applicationMulti-spectral CTMagnetic nanocompositemotion parallaxMultilayer GraphMixed RealityMEASURING GEOMETRYMulti-user DisplaysMirror Replacementmultiple viewpoint imagesMHEALTHMaximum Likelihood Classifiermultiview stereomulti-target trackingMULTI-TAP PIXEL STRUCTUREMLPmid-level visionMEASUREMENTMULTISPECTRAL LIGHTINGmapsmulti-viewMaterial PhysicsMOBILE TEXT ACQUISITONMusic IconographymodelingMULTI-ILLUMINANTMPEG-I Visualmulti-task networkMetamericmobile VR controllerMachine-learningMean average PrecisionMagic LeapMulti-Light Image Collection(MLIC)MAJORITY VOTEmicroformmHealthMobile LearningMobile imagingMobile Ultra-broadband NetworkMobileMagnitude estimationMATERIAL-LIGHT INTERACTIONSMULTI-CHANNEL PRINTINGmosaic imagemultisensorymotion characteristics of 3D videosMIRRORMotion estimationmulti-scale featureModified RANSACMolecular BiologyMULTI-VIEW IMAGINGMTF50PMRFmap generationmultilabel graph-cutMacro-uniformityMOBILE HEALTHCAREMULTIMEDIA RETRIEVALMachine Learning Applications in ImagingMOVING OBJECT DETECTIONMobile PhoneMATERIAL APPEARANCEmachine learning applications in ImagingMultiple wavelength tracingmulti modalitiesMicrocomputerMulti-view Processing Unit (MvPU)Monitor CalibrationmodelsMobile ImagingMEMORY INHERITANCEMulti-camera visualizationMultispectral imageMOTION VECTORSmachine perceptionMULTICAMERAMicrocomputer clusterMICRO 3DMODULATION TRANSFER FUNCTIONMULTI-APERTUREMANIFOLD LEARNINGMotion vectorMotion Correction PerformanceMULTILINGUAL LECTURE NOTESMasked PixelModel TrainingMODE DECISIONMOIRE FREEMonocular Depth EstimationMobile VR interfacemeasuresMACHINE LEARNING CONCEPTSMetricsMUTUAL INFORMATIONMulti-view data integrationmental mapsModulation Transfer Function (MTF)MULTI-VIEW IMAGESMULTI-VIEWMaterial appearancemetamerMULTI-REFERENCE PREDICTIONmaterial validationmetallic objectssMACBETH COLOR CHARTSMobile DevicesMULTIPLE CUESMetricMULTISPECTRALMass Spectrometry ImagingMULTIPLE VIEW DEPTH GENERATIONMultispectral ImagingMEDIEVAL MANUSCRIPTSMulti-exposure ImagingMulti-GPUMultispectral imaging methodMOSmaterial classificationMULTI-SENSORY FEEDBACKMultiple sclerosismotion sicknessmobilemodel-based imagingMICROSACCADEMOTION CAPTURE DATAMULTI-SCALE APPROACHMACHINE LEARNING FOR IMAGES AND VIDEOMedical Image PerceptionMemory ColorsMaterial designmass digitizationMonochrome layerMICE IndustryMEDICAL HEALTHCAREMicrofabricationMOTTLEMedical ImagingMATERIAL EDITINGmetallic surfacesMETRICS VERIFICATIONmobile imagingMAGNIFYING OPTICAL SYSTEMMultimodalMULTIMEDIA FORENSICSmixed realityMultispectralMOTOR LEARNINGMEMS SCANNER BASED MOBILE PROJECTORMobile DeviceMorphological OperationsMULTI-DIMENSIONAL ERROR MINIMIZATIONMedia ArtsMULTISPECTRAL CAMERA
N 
NVIDIA Jetsonnon-visual face empathyNash equilibriumNOISE REDUCTIONnavigationNatural scene statisticsNonuniformly samplingNormal MapNEURAL MODELnailnaturalnessNON-LOCAL REGULARIZATIONnetworked medianingunismoNanocompositesNonlinear Inverse ProblemsNVIDIA VISUAL PROFILERNeural NetworkNight ScenesNext Best Light PositionNANO-CELLULOSENukeNeural networknear-infrared imagesno reference experimentNCS hueNS-SFRnon-invasive spectroscopic techniquesnatural image statisticsnew mobilityNonacellNoise Power SpectrumNear infrared face recognitionno-reference quality assessmentNORMAL VECTOR IMAGINGNumerical SimulationNon-LambertianNext Best Light Position (NBLP)Notch featurenon-local moduleNon-visibleNEURAL ACTIVITY IMAGINGneural spatial processingnon-linearityno reference metricNatural Scene StatisticsNEUGEBAUER PRIMARYNEUROPLASTICITYNaturalnessneuroaestheticsneural networksnoncontact measurementNEWTON'S ITERATIONNon Local MeansNano PrismNVH Simulationnonlinear inverse problemsNext generation displaysnormal vector to a 3D surfaceNatural Language ProcessingNeRFNoisy labelsNeural NetworksNEUROSURGICAL TREATMENT PLANNINGnon-uniform illuminationNOISENoise robustnessNETWORK CAMERANGTnoiseneural fieldsnear-infraredNursing Educationnon-linear maskingno-reference image visual quality assessmentNISNet3Dnon native contentnonuniform optical responseNaturalistic Driving StudiesNR-MVQANRnuScenes datasetNoiseNEQnumerical simulationsnoise reduction.No referenceNATURAL USER INTERFACENeural RepresentationNewton methodNetwork confidenceNoise power spectrumNoisy point cloud filteringnoise equivalent quanta (NEQ)NUMERICAL METHODS ON LIE GROUPSNatural steganographyNAÏVE BAYESNATURAL LANGUAGE PROCESSINGNoise eliminationneural transformationnonuniform image procesingNormalizationNO-REFERENCE MODELNPSNEGATIVE GATE BIASLESSNutritionnon-linear-smoothingnoise modelnonlinear image processingnoise power spectrumNEURAL NETWORKSNO-REFERENCENoise Equivalent Quantaneuroscience and artnetworkingnoise power spectrum (NPS)Noise evaluationNovel vision systemsNo-referencenano-silvernon-visual learningNon-invasiveneural networknatural scene statisticsNovel AC Method to Drive High Temp FDM HotendNON-LINEAR DISTORTIONno-reference image quality modelNeural network hardwareNovel imaging modalities and sensorsnear infra-redNext Best Light PositionsNoise equivalent quantaNo-reference quality metricNOISE FREE TEST IMAGE DATABASENONLOCAL TOTAL VARIATIONNR Quality AssessmentNeural RenderingNONLINEAR TRANSFORMATIONNavigationnon-negative matrix factorizationnatural languageNLPNEURAL NETWORKNeural networksnaturalistic driving studiesnon-cooperative gameNEUROREHABILITATIONNEAREST NEIGHBOR ALGORITHMNear-infrared (NIR)Noise reductionNEGATIVE DISTORTIONNAVIGATION METAPHORSnumerical pathologyNEAR-SENSOR IMAGE PROCESSINGNon-linear optimizationNATURAL IMAGESnoise equivalent quantaNuclei Segmentationnear point distanceNO-REFERENCE IMAGE QUALITY ASSESSMENTNATURAL IMAGE MATTINGNon-BlindNumerical ray tracingneighborhood components analysisNegative groundnoise imageNona BayerNANO-MATERIALSNatural SceneNR-IQAnozzleNext Best Viewnip pressurenon-visual face perceptionNoise cancellationNi-based alloysNeugebauer Primary Area CoverageNaive Bayesnatural scenesNETWORK SECURITYNODE CONNECTIVITIESNON-GRID POINTnumerical robustnessNeurosymbolicNEURON DETECTION ALGORITHMnetworkNatural language processing
O 
online psychophysicsObject detectionORANGE PEELOrganic Filed-effect TransistorsOptical AberrationON and OFF cellsOCCUPANCY GRIDObjects of interestONTOLOGIESORB_SLAM2object trackingOBJECTIVE METRICOne-Class ClassifierOptical Character Recognition (OCR)over exposure correctionObject DetectionONBORD CAMERAObstacle DetectionOn-line Deep LearningOmnidirectional VideoopticsObject recognitionOptical imaging systems and lensesOUT-OF-BAND RADIATIONOBJECTIVEocclusionOBJECTIVE TECHNICAL QUALITY MEASUREMENTOSINTOpen-Source ToolsObjective and subjective evaluationObjective quality metricsover-segmentationOptical SystemsOpen Video CodecsONLINE SOCIAL NETWORKOPTIMUM FREQUENCY BAND PARTITIONoptical instrumentsOutdoor surveillanceON and OFF neuronsOBJECT RETEXTURINGoptical distortionoptical detectionOpenColorIOOptical profilometryOculus Quest 2outlier filtrationOLED paneloof psfopacityonlineOBJECTIVE METRICSoptomechanicsOprimizationOmnidirectional VideosObject detection dataomnidirectional imagesOrnithologyOMNIDIRECTIONAL VIDEOOmnidirectional contentoriginal camera outputOmnidirectional imagesontologiesOBJECT EXTRACTIONObservers BehaviorOptimizationOWASPOPTICAL FLOW ANALYSISONTOLOGYobject segregationOptical resolutionOUT-OF-FOCUS BLURout of distributionOutlier detectionopen-source intelligenceoptical systemoptimizationobservation systemobsolescenceOMNIDIRECTIONAL CAMERAOLEDOPTIMAL BORDEROSINT InvestigationOpticsopen source intelligenceOPTICAL CHARACTER RECOGNITION SOFTWAREOBJECT IDENTIFICATIONOPENCOLORIOold photographsOPTIMIZATIONONLINE MUSEUM FOR SELF-IMPROVEMENT (OMSI) NEURO-PHENOMENOLOGICAL/EPISTEMIC APPROACHOBSTACLE AVOIDANCEopen sourceOmnidirectional videoOPRoptical filter controloptical see-through AROBJECT SEGMENTATIONOBSTACLE DETECTIONObjective image qualityobject removalONLINE TRACKINGopponent color theoryoptical waveguidesoctenyl succinic anhydrideOptimal LearningObjective measurementOmnidirectional Imageobject detectionoptical flowover-exposureOBJECT RECOGNITIONObject RecognitionOxygenationOWASP IoT Top 10oilorientationObjective quality assessmentoptical quality controlonline fashion marketplaceOUTLIERSOPTIMAL TRANSMISSIONON-CHIP ANALOG MEMORYOCRObject Trackingorphan-pagesOBJECTIVE IMAGE QUALITY METRICOmnidirectional CameraOn-street parkingOOPontologyOBSERVER METAMERISMOtsu thresholdobject recognitionOptically Variable DeviceOPEN SOURCEOCTOptical flowObject ReconstructionOCULARITYObjective Evaluation MethodOral Cancer ScreeningOpen-source softwareON-THE-FLY PERFORMANCE EVALUATIONONLINE EDUCATIONOPTICAL METROLOGYOptical FlowObjective Testonline model estimationOseberg tapestryONLINE LEARNINGOptimisationOPEN SET RECOGNITIONopen source toolsobservation distanceOBJECTIVE IMAGE QUALITY ASSESSMENT METRICSOculus Headsetopponent processesopen wireless networkOpenVSLAMOCCLUSIONoled displaysOPEN ACCESSoptical character recognitionoptical system designOUTPUT STRIDEON-DEMAND ELECTROSPRAYINGobserver metamerismOptical modelON-SCREENOPHTHALMOLOGYOPTICAL FLOWOUT-OF-GAMUTOceanoptical characterizationOPTICAL SYSTEMOBJECTIVE TESTINGOBJECT RECOGNITION AND SEGMENTATIONOCIOOpacityOn-line fashion imagesOFDMorganic light emitting diode (OLED)OPTICAL DENSITY FADINGOBSERVER CALIBRATIONoledOpenVxOver-exposedOcean DroneOCR systemsOpen Source IntelligenceOpen ArchiveOUTLIER DETECTION (OD)OPEN ENVIRONMENToptical brightenersOptical QualityOptimal Colorsone shot cameraOCTONION DISCRETE FOURIER TRANSFORMONLINE MUSEUM COLLECTIONSOCR PERFORMANCEOnline trackingOcclusion areaORIENTATIONObserver MetamerismOCCLUSION STATEObject based video forgeryOcclusion handlingorange peelObject DistanceOCULUS RIFTOPERATING ROOMObjective Quality MeasuresOCCLUSION DETECTIONOPTICAL CHARACTER RECOGNITIONObjective image quality assessmentOUTLIER DETECTIONOut of focus blurOptical vignettingORGANOMETAL HALIDE PEROVSKITE
P 
P1858pyrolysisPre- and post-treatmentplasticspuzzle solvingpartial encryptionPythonPhotometerPOWDER-BASED 3D PRINTINGPerceptual metricPOLARIZATION MULTIPLEXINGpublic spacePERCEPTUAL QUALITY EVALUATIONPixel designpulse ratePERSON RE-IDENTIFICATIONpaintPSYCHOPHYSICAL EXPERIMENTSParallax CoherencePattern recognitionProjectorpiezo self sensingPARTICLE DATAPhotographypolarization imagingPRINT IMAGING PIPELINEPrinting Defect Detectionpreservation effectPHYSICALPassive Stereo VisionPoint CloudPAPER-BASEDPRESERVATIONPerspective TransformPERIODIC DISTURBANCEpeak luminancePseudo labelingProjection type light field displaypersonal experiencePERCEPTUAL COLOR IMAGE COMPRESSIONPytorchPrecisionperformancePhoton-limited imagingPROBE DETECTIONPrecipitationPrint QualityPseudocolorPRIMARY SELECTIONPrinciple pointPSYCHO-VISUAL TESTpuzzlePHOTON SHOT NOISEPRINTINGPerson re-identificationPCB DefectPENETRATION TESTINGPose verificationPOINT SPREAD FUNCTION (PSF)Photo-Response Non-UniformityPeri-FoveaprocesiingPhoto-response non-uniformityPVC printingpassport controlPhase-shiftingPERCEPTUAL INTELLIGENCEPARTITION SCALING METHODOLOGYPlant Width EstimationPoly-jet 3D Printingprobabilistic graphical modelspublic speaking trainingprivacyprintsPOLYNOMIALPower constraintsprefetchingpurplePrinting Iridescent ColorsPixel-shiftPoint Cloud DataPatternPrompting SteganographyPHOTOMETRIC FEATURESPerceptual approaches to image qualityparticipatory culturePOWERPublic accessPhotographposturePRINTED- ELECTRONICSPoint cloud denoiseprefer skin colorPOWER SPECTRAphysics inspired machine learningperceptual spacesprotanPANORAMIC VIDEOProximal MappingPOSE ESTIMATIONPrediction algorithmsPTMpill colorPATH PLANNINGPRIMARY COLOUR EDITINGProbabilistic modelingprint resolutionPen Testingperceptual information hidingPhotorealisticPHOTOGRAPHYPOINT-SPREAD FUNCTION (PSF)parchmentPedestrian collisionPATCH-BASED SYNTHESISPoint cloudspsychophysical studypsychophysical methodsPaintingpolychrome Barcodepoint cloud dataPAIN DISTRACTIONPreservationperceptual uniformityPage DefectsPROJECTION ENGINEPerformance Metricsperception of distancePhotomechanicalPALM VEINPlayer labelingPointcloudPHASE IMAGINGPERCEPTUAL QUALITYPhase detection autofocuspFibonacci numbersPeople recognitionPROJECTOR ARRAYPolarizationPRINT-AND-SCAN PROCESSPLENOPTICSProtected workshopsParameter OptimizationPlant Image ProcessingPSYCHOPHYSICAL EXPERIMENTphase retrieval algorithmPerformance analysisPlane and curved fluorescent objectsPhoton shot noisePHOTORECEPTORSPerson Re-IdentificationParticipationPerson Re-identificationpathology imageprint qualityParallax BarrierPerspective ShiftPAIR COMPARISONPRNUPERFORMING ARTSPHOTON TRANSFER NOISE ANALYSISPrinterphotosPAIRWISE COMPARISONSPolarization gratingPaper's propertiesPENTESTINGPrinting QualityPanoramaprint marblePath-tracingprinter healthPeripheral Visionpose estimationPSYCHOPHYSICSPrinted DefectPhotometric stereopixel-based image differenceperception mechanismpassport photo manipulationpacking paperPoint Spread Function PSFPassive 3DPTZ cameraspattern recognitionPARALLAX BARRIERparameter-free attention mechanismPROCESSING HISTORY RECOVERYpaperPERCUPTUALL LOSSLESSpose analysisprotanopiaPROJECTORPHASE DETECTION AUTOFOCUSportable document formatpreservationPlug and Play priorPAINTINGSPerceptual BiasPsychophysical experimentPigment classificationphotocuringprint reproduction differencep5.jsPhotodiodes, Pixels, and ProcessespolarizationPassiveTotalPAIRWISE COMPARISONS SCALINGPRINTHEADSparallel coordinates plotsPLS-SEMPedestrian behaviorsPRODUCT PHOTOGRAPHYphysiological signalspoint light source modelPrintingPostprocessingPOLYANILINEPoint Cloudspest controlPrinter ForensicsPlug-and-Play priorsPrintparamerpedagogyPROJECTION BASED AUGMENTED REALITY SYSTEMPRINCIPAL COMPONENT ANALYSIS (PCA)Patient monitoringpost-cataract experiencesPOSE PREDICTIONPerceptual QualityPhysiological MonitoringPrintabilityPhotogravurePHOTOGRAMMETRYPOSITRON EMISSION TOMOGRAPHYperceptual experimentPedestrian IntentionPlant Height EstimationpsychophysicsPoint cloud alignmentPoisson-Gaussian noisephotodiodes, pixels, and processesPRETREATMENTPERCEPTUAL IMAGE QUALITYPERCEIVED DYNAMIC RANGEPIGMENTPerceptual learningPrinted products enrichmentPHASE-SHIFTPHOTOREALISMprivacy preserving forensicsphotonspatinasParallel Coordinatesprint head designPerceptionPhase detectionPSYCHOVISUAL RATE-DISTORTION OPTIMIZATIONprintingPHOTOMECHANICAL REPRODUCTIONprogressive GANpedestrian dynamicsprinted electronicsPSYCHO-VISUAL EXPERIMENTAL SETUP|PARTITION SCALING METHODOLOGYPIXEL ERROR MODELPowerPOSITRON EMISSION TOMOGRAPHY (PET)Pixel Scalingprinter modelphotographyPiece-wise-linear rampP2020POLARIZED LIGHT CAMERAPRIMITIVE SHAPEPRIVACYPRINT FADE DETECTIONpaintingPerception and AnalyticsprecisionPARplasticityPRE-PROCESSINGpixelPoint light source arrayPerceptual UniformityPeripheral SensitivityPENALIZED-LIKELIHOOD METHODPYTHONPedestrian detectionPoint-spread functionperformance evaluationPhase shiftPrinter Identification systemPainting Material RecognitionPATIENT SPECIFICITYPHASE-CODED APERTUREPatient Assesmentphase estimationPRINT COLOR FADEPoint cloudPHOTON FLUCTUATIONPrinted image qualityPSEUDO-HAPTICPlace recognitionPigmentsPseudo Video SequencePATTERN ILLUMINATIONPHOTODIODESPALIMPSESTParallelizationpotentiometric nitrate sensorPERCEPTUAL MATCHINGPoint spread functionpainting authenticityPerspectively Correct Surround ViewPHOTODIODES, PIXELS, AND PROCESSESPose Estimationperson detectionparameter optimizationPHENOTYPINGPERCEIVED QUALITYPerspective correct surround viewperceptual color mapsPerformance predictionPSNRpigment identificationpolynomial regressionPERCEPTUAL COLOR MODELINGPhenomicsPhotogrammetryPRODUCTION OF LECTURE NOTESPassive-Aggressive classifierpupil sizepiezo self-senfingPicture qualityPhotoplethysmographypupil diameterPLAYBOOKpressure sensorPrivacy and ForensicsPixelsPrinted Electronics Electroluminescent Multiple layersperceptual qualitypresencePeer to peer communicationPERCEPTIONphoto manipulationpupil detection and trackingPrincipal Component AnalysisPrinting differentiationPCB SURFACE FINGERPRINTINGPHYSICAL OPTICSPACKAGINGParticle filteringphase unwrappingProgrammable cameraPolymer hybrid materialsprinter mechanism controlPatentsPHASE CORRELATIONPERSPECTIVELY CORRECTNESSPDAFphoto-response non-uniformityParchment stabilizationPHASE CONGRUENCYPerformance evaluationpolychrome barcodeProduct AssemblyPortraitPhoto-finishing methodsPUPILLOMETRYParticle filter object trackingPUPILphotometryPAPER WHITEPRINT IMAGE QUALITYPOLARIZATIONPhase extractionPOSE TRACKINGphotographic booksProfile Connection Space; ddghdhgPOINT CLOUDPrivacy IssuesProcessespreprocessingPanoramasPRINTpreservation intangible cultural heritage digitization image video audio website repositoryPixel Evaluation MethodsPRINT QUALITYPROXIMITY CUESPara-FoveaPsychophysicsPHENOMICSParkinsonianpersonal preferencesPLANAR ABSTRACTIONPERCEIVED SHARPNESSPHOTOMETRIC STEREOPASSIVE ELBOW MOVEMENTPolychromeparticle swarm optimizationpaintingsProcessing HistoryPERSON SEGMENTATIONpowder clusteringPerformance assessmentpixel modelPhase Retrievalplenoptic cameraPackagingpiezoelectric single-pass inkjet printingPEDESTRIANDETECTIONPerceptual qualityprintPapanicolaou stainPrincipal Component Analysis (PCA)Phase retrievalPEER-TO-PEER (P2P) NETWORKSPointing TechniquesPhoto-realisticPeak luminance distributionphase congruencyperceived image qualityparticle sortingPERCEPTIBLE RANGESphysiological responsesPEDIATRIC ONCOLOGY PATIENTSpigment lightfastnessPlanckian illuminantpracticalprocessing fluencyPrivacyPERIPHERAL VISIONPoint Cloud RegistrationportraitPAGE CLASSIFICATIONPROCESSING HISTORYPROBE RECOGNITIONPrinted PagesPathogen detectionPEAK LUMINANCEPERCEPTUAL TRANSFORMSPICTORIAL IMAGE TARGETpressurePhoto-response non-uniformity (PRNU)PPGPOINT GRIDportraiture analysisPerceptual Video QualityPhase Detect Autofocus (PDAF)perceptual approaches to image qualityperceptual aftereffectsParticle Swarm Optimization (PSO)Perspective projectionPhotodiodesplug-and-play (PnP) reconstructionPartial ViewPain DistractionParametric effctPrint qualityperceptibilityPHENOTYPE DATA COLLECTIONPerformancePIXELSPose estimationpractice-led designperceptionperspective analysisPattern RecognitionPhoto Archivespoint cloudPROFILINGPHOTON ABSORPTIONPoint Spread Functions (PSFs)PRINCIPAL COMPONENT ANALYSISPATTERN RECOGNITIONPrintsPackagePREFERRED COLORPOCSPseudo-referencePedestrian Behavior AnalysisPERFORMANCE COMPARISONPortraitsPerceptual trainedPrinting Velocity Variationphotometric stereoPOOLINGPHYSICAL DISPLAY PARAMETERSParameter EstimationPERFORMANCE ANALYSISPan-sharpeningPoint source localizationPSYCHOGENESISPERCEPTUAL EXPERIMENTATIONPokemonpoint spread functionPROBABILISTIC MODELINGpulse wavePrint defect detectionPaper-basedpapyruspre-distortionpassive markersPRINTSPREDICTIVE PARAMETRIC IMAGE COMPRESSION CONTROLPERCEPTUAL APPROACHES TO IMAGE QUALITYPARTIAL ENCRYPTIONPhotographingPooled SteganalysisPHOTO BOOKSprivacy protectionPORTRAIT AND LANDSCAPE MODEPERCEPTUAL COLOR GAMUTPSF ENGINEERINGPHOTO-ELECTRIC AND COMPTON DECOMPOSITIONPERCLOSphase retrievalphotogrammetrypsychometric functionperformance predictionPHYSICAL ACTIVITYPLANARITYPenetration Testingperceptual stimuliProsumer Multimedia StreamPRE-TRAINED CONVOLUTIONAL NEURAL NETSpost-processingperspective
Q 
QUANTUM DOTquadratic programmingquality metricQuality LossQuality factorsqoeQuality controlQuaternionQuality PerceptionQuality AssessmentQuantitative SteganalysisQuality MetricsQuality MonitoringQuantum efficiencyqualityquality of experiencequantizationQuantum imaging and photon-efficient techniquesQuality of ExperienceQuality of image in virtual realityquality assessmentQR CODEQUALITYQualitative analysisQuality of Experience (QoE)quality controlQuantitative metricQuality metrics, full-reference, no-referenceQUITXTquick-response liquid powder display (QR-LPD)qr codeQuality of appearancequaternion gradientsQUATERNION DISCRETE FOURIER TRANSFORM/kwd> COLOR IMAGINGQuantum EfficiencyQuality assessmentQuantum efficiency (QE)quaternionQOEQuality EstimationquantitativeQoEQUANTUM YIELDQUALITY OF COMMUNICATIONQuad Bayer Color Filter ArrayQuantitative analysisQUATERNION DISCRETE FOURIER TRANSFORMQuick response (QR) codesquality of immersivenessQUALITY OF EXPERIENCEQuad BayerQuantification Methodquality metricsQUALITY ATTRIBUTESQuantizationQUALITY ASSESSMENTquality assuranceQUALITY ASSURANCEQUALITY LOSS JNDQUALITY RULERQualityQUALITY AWARE FILTERSQUANTITATIVE SPORTS ANALYSIS
R 
RANGE SHIFTRelocalizationReal 3D objectRate-distortion optimizationRadiative Transfer Equationrecursive group codingREMINDERSRobustnessRGBD FUSIONred-green color vision deficiencyRelay LensRewriteable digital tagRECONSTRUCTIONReinforcement learningROCKET STARTRECONNAISSANCEReference picture resamplingRiskIQ PassiveTotalRoad Segmentationresidual networksReal-Time RenderingresolutionREGULAR BANDSremote sensingREFLECTANCE ESTIMATIONRECAPTURINGRetailred and green confusion peopleRARE EVENTSRe-trainingRegion of interest (ROI)RE-WRITABLE INFORMATIONRetinal blurreceptive filedRenderingrepresentationRelative humidityRAWRealtimeREAL-TIME FEEDBACK VIA VISUAL ANALYSISROTATING TABLERAPID PRESENTATIONReproduction accuracyRobust HashRecurrent Neural NetworkRobust registrationROBUST OPTICAL DESIGNremote tutorialsreference printing conditionsREFLECTION MODELRTS NOISERGB gamutRELIEFrecognition-aware learned compression methodRandom ForestRAW COLORResource constrained displaying solutionsRANGE CAMERAremote vision systemResinRadiation OncologyRen\'e MagritteRADIATION DETECTORRTI -Reflectance Transformation Imagingreligious symbols and attributesRAW imageregression analysisREVERSIBLE DATA HIDINGRegion of Interest SelectionREFERENCE SENSOR PATTERN NOISEROLLING SHUTTER IMAGE-SENSORRGBDrawtoacesrotogravureReliefradiometryRadiance Image RenderingReproductionRailroadROLE OF TEXTURE INFORMATIONRingingReal-Time Image ProcessingRespiration rateREAL-TIME DETECTIONRADIUS OF CURVATURERobust Localizationrobot manipulatorsRAY TRACINGRadarretinexRGBN imagesRECOMPRESSIONReduced-Referencerobust optimizationRAYCASTINGRadiologyReproduction of Material AppearanceRAINDROP DETECTIONrheologyRECEPTIVE FIELDROUND TRIPREAL-TIME CONCURRENT DISPLAY AND IMAGINGROUND SENSORrobust metricsRelightingReal-timeReflectance Transformation ImagingReconstructionrefocusRGB printingResidual signalsremoving stray-dotsregional maskingReset noiseReverse engineering of deceptionsROBUST HASHINGRobustness of Deep neural networksRGB-NIRre-IDRadar for depth estimationRange ImagesROBOTRAW IMAGEROBOTICS COMPETITIONSREACTIVE GRASPINGROBUST COMPUTATIONAL IMAGINGreconstructionRay tracingrobust classificationRGBRGB-WHITERate-distortion optimization (RDO)router forensicsROBUSTNESSRegressionReflectance transformation Imagingrisk managementrecognition of hazardous materialsRotation angle estimationRF SignalReference Sensor Pattern NoisereflectanceRegistrationRelevance FeedbackReal-time view synthesisremote collaborationreflective colour chartreceptive field expansionroad maintenanceRGBD SENSOR ARCHITECTURERegressorROI CLASSIFICATIONResolving powerREAL TIMERED LIGHT IGNOREDRGB & NIR cameraregular synthesis of a bit signal without window processingrapid prototype developmentrecognitionremaining shelf life predictionremote maintenance protocolreflectance estimationRECTO-VERSO PRINTINGRAYLEIGH SCATTERINGRDArepeated cross-validationrate controlROBUST METRICSRaspberry PiRemote controlled lab based moving platformRGBD dataREAL-TIME ADAPTABILITYretention and drainageRGBD PROCESSINGRE-WRITABLEReflectance measurementRestorationreal-time communicationRegulationsRetinaNetradiation therapyRGBWREFLECTION AND LUMINESCENCEReal-time 3D reconstructionroad passabilityreinforcement learningRinted materialrub resistanceresidual connectionRobust Hashesrandom dot stereogramregion descriptorsRUN LENGTH DESCRIPTORRANKING SVMRELIABILITYResampling detectionrPPG predictionRelative Standard Deviation Area (RSDA)Rate distortion optimizationreversible adaptive watermarkRadianceRay TracingRobust hashingrednessREAL IMAGEREGULARIZATIONROUGHNESSRec. 2100REFERENCE IMAGERedditradiometric correctionRECOLORINGRefocusre-trainingrail tampingROLE OF STRUCTURE INFORMATIONRandom Forest classifierremote sensing imagesRESIDUALresearch processReflectance Transformation Imaging (RTI)radiographyROIred-green confusionrelightingreal-world visionREAL TIME DATA CAPTUREreceiver operating characteristicretinal imagerestorationRecursive LearningReflectance transformation imaging (RTI)REAL WORLD TRAFFIC DATA SETRandom FernsRecognitionRemote SensingRemote vison systemROBOTIC SCRUB NURSERANSACRTI datasetROBOTICSReading orderrandom CFARECURRENT NEURAL NETWORKRGB-IRred scalergbwRisk PredictionRadiance FieldsrealnessRETINARobust HashingRemote vision systemReflectancereal timeRay-tracingroad boundaryrate-distortion lossREINFORCEMENT LEARNINGROOM BRIGHTNESSRESPONSE CURVERANGE RESOLUTIONregularized gradients domainRaw ImageReal Scene ExperimentREGRESSION ANALYSISRole-Playing GameRHEUMATOID ARTHRITISRobustness Evaluationrenewable energyRace Biasrobust hashRotation invariant featuresRECOGNITIONrounding errorRetinexRibbon SnakesregressionRed TeamReal-world computer visionRADARRemote PhotoplethysmographyREFLECTANCEREMOTE DIAGNOSISReviewreal-time pedestrian detectionReal-time Applicationsregularized gradient kernelRealistic image quality chartsRAW SENSOR IMAGERainRewriteable informationREVERSE ENGINEERINGRelationRENDERINGreproduction of material appearanceReproducible researchRGBW CFARecyclingRadon transformRadial basis function networkRegion of interstrobotic armRGBW Color Filter ArrayRGBD IMAGE EXTRACTIONREGISTRATIONRTIrobotRadar as a supervision signalRANDOM FORESTRESOLUTIONREFLECTION TRANSFORMATION IMAGING (RTI)RoboticsroboticsRadiance Imagerotation estimationrobotic systemsrouter securityROBUST PCARANGE LINEARITYreal-timeRETINAL PROJECTION DISPLAYrepresentative colorRepresentational dissimilarity matrixReal Time Applicationraw imageResolutionREFLECTIONremote heart rate measurementRamp ADCRasterREAL SURFACES
S 
spectral predictionsteganalysisSecure Convolution Neural NetworkSpatial DistributionSPECTRAL RECONSTRUCTION FROM RGBSPATIAL COGNITIONsensors and processorsStray lightSD&A conference program insightsspectral image projectorStructure from motionskinSTEREOSCOPIC 3D IMAGESSports strategy analysisseven segment displaySTEREO VISIONscale-spaceScanner Image ProcessingSource identificationSPACE-VARIANT SMOOTHINGSpatial and Nonspatial Visual IntegrationSurface appearanceSimilarity perceptionSECURITY PRINTINGSOLAR ECLIPSE VIEWINGSLANTED EDGESUBSPACE LEARNINGsteel defect detectionSystem on Chip (SoC)STABILITYSMART PIXELS SENSORscreened PoissonSemantic information in SLAMSurgical Task Assessmentscene understandingSTEREOSCOPYStereo disparity estimationSOFT ROBOTICSSVRSPORTS CULTURESUBPIXEL STRUCTUREsocSurface scienceSimultaneous localization and mappingSaliency RegionSPYWARE, MALWARESteganographyself-poweredsalient region detectionSelf-supervisionSemi-mobile Display SetupShadow detectionSMART IMAGE SENSORSSEMANTIC SEGMENTATIONspatially correlated noiseSENSITIVITYStructure tensorSelective codingStreamingSystem Power OptimizationSYNTHESIZED VIEWsurface reconstructionstrain sensorsSCATTERING POLARIZERspecular reflectionSPECTRAL REFLECTANCESiL/HiLSHOOTING DIRECTION CONTROL CAMERAStarch U-netStereo thermal cameraSTEREOSCOPIC IMAGESsource crowdingSemi-automatic video segmentationSemi-fragilesecurity self checkSupernovaescatteringScaling estimationSUBJECT TRACKINGSPATIAL-TEMPORALscore-based likelihood ratioShooting time lagSTEREOSCOPIC CONTENT PRODUCTIONspatial cognitionSURFACE REFLECTIONSALIENCY-BASED CRITERIASURFACE TENSIONStereoscopic Content ProductionScattering transformSPECTRAL DATASKELETON-BASEDStack-based imagingSkin healthSERIOUS GAMEstereo matchingSPOOFING ATTACKSmoothness Constraintsystem performanceSubjective Video Quality AssessmentStitchingsubsurface light transportScheimpflug imagingSubjective experimentsmartphoneSensor SimulationSIGNAL TO NOISE RATIOSkewed Imagespecular glossSeismic data recoveryStreakSAMPLING SPARSITYStyle colorizationStein's unbiased risk estimationSignal to Noise RatioSUPER MULTI-VIEWSun trackersSENSE AND AVOIDSINGLE ANGLEstyle transferstorytellingSTATISTICAL LEARNINGSYSTEM GAMMASEEING AND READINGSentiment DetectionSource camera identificationSUPERPIXELSScanpath predictionSemi-automatic Video Annotationspectral sensitivity functionsslanted starSPECTRAL MEASUREMENTSupervised learningSIMILARITY MEASUREMENTSpectrogramsSPECTROPHOTOMETRYSoft-proofingSCANNING DOME ILLUMINATIONStereoscopic DisplaysSimulated Long-Range TestingSimulator SicknessSpeech emotions RecognitionSURFACE STRUCTUREscene-type dependencysubjective qualitySTEREOsensorssensor designSENSING AND IMAGING TECHNIQUESSUBJECTIVE TESTINGShort-term facial pore simulationself-regulationsaliencysubsurface scatteringsynthesized speechshearletsituational awarenessSkin feature detectionScreen PrintingStructure-Aware HalftoningSPECTRAL VS. SPATIAL PERFORMANCESKELETAL MATURITYSmall angle scatteringskip connectionsustainabilityStandardSOFTCOPY QUALITY RULERstereoscopic, VR, and true 3D displaysSKIN COLOURScanned Image RegistrationSurround view automotive systemsSpeckle Estimationspreading speedspontaneous problem-solvingSmall Pixel CISSTNSOCMINTSYSTEM PERFORMANCEScalable Spatial Pyramid Pooling (SSPP)smart homesurfaceSubjective testingSubjective EvaluationSoftware solutionsSNR10SKIN COLOUR PERCEPTIONstain detectionStaircase Gelb illusionSubjective data collectionstatistical characterizationSHAPE FROM FOCUSsingle photon avalanche diodeSINGLE-CHIP IMAGINGSharpnessSubjective QualitySegNetsupervisedScene-and-Process-Dependent Modulation Transfer Function (SPD-MTF)Simulated DistanceSyndrome Trellis CodesStereoscopic, VR, and True 3D Displaysshape depth reconstruction deep learning fluids specularsecure remote controlStereo renderingSUBJECTIVE AND OBJECTIVE QUALITY ASSESSMENTSTEREOSCOPIC CINEMA AND TVStereoscopic DisplaySECURE PAYLOAD ESTIMATIONSUPERCELLsynthetic imagerysemantic image analysisSystem TopologySpecularitySpiral descriptorSHOOTING TIME LAGsmart energy houseSMARTPHONE IMAGINGSPECTRAL ESTIMATIONSPARSE DATAskillsSTEREOSCOPIC CAMERASCALE SPACE HUE FILTERINGspectroscopySpectral reproductionSEAM CARVINGSATELLITE IMAGESSIDE-INFORMATIONSurface roughnessside informationSTEREOSCOPIC IMAGESemantic labelsSECURITYSystem PerformanceSYNCHRONIZATION ARTEFACTSSVHNsignal processingstereosopic displayscreen printingSubband decompositionSPECKLESUBJECTIVE STUDYSTEREOPSISScene-and-Process-Dependent Noise Power Spectrum (SPD-NPS)SEE-THROUGH DISPLAYspatialSwitchingstate authority archivesSKY DETECTIONstereo-blindnessSubjective evaluation experimentSparsityspeech forensicsScene LabelingSPECTRAL IMAGINGsimulation validationSPECTRAL RECONSTRUCTIONStereoscopic Human Factors and DesignSlow motionSeam shapesuperpixel decompositionServerlessSubjective Quality DatabasesSecurity imagingStaircase method.STEREO ACUITYsubjective evaluationSTEREOSCOPIC 3Dstereoscopic qualitySearch VisualizationSPHERICAL IMAGESparse SamplingStar ratingsstress indexSplit PhotodiodeSPECTRAL ANALYSISSUPERCAMERASkySPORTS ANALYSISSensitivitySplit-Bregman optimization methodSWITCHABLE DIFFUSERSLMSpatio-Temporal ModelSystem IntegrationstabilizationSalient Cuessensor linearizationstacked diodesSignal-to-Noise Ratio (SNR)security operationssamplingSCALABILITYsupervoxelStructured lightsmart gridstereoSensorsShitsukanstereoscopic imagesSpace ApplicationsSUSTAINABLE DIGITIZATIONSALIENT POINTSsensorSUBJECTIVE QUALITYSensorSkin ColorSparse recoveryshapeSUPERVISEDstereoscopic human factors and designsurrounding illuminationSPECULARITYStandard updateSTOP MOTIONSiamese NetworkStreak Detectionstereoscopic cinema and TVSELF-DRIVINGSpectral Filter ArraySecond Harmonic Generation Imagerystereoscopic, VR, true 3D displaysSMART CITYSkeletonsimulator sicknessSIMULTANEOUS CONTRAST EFFECTsimilarityStereoscopic PhotographySIMULATOR SICKNESSSINGLE-IMAGE SUPER-RESOLUTIONSCENE SEGMENTATIONStereo ProcessingSOFTWARE DEVELOPMENTSupport Vector Machine (SVM)Semantic Gaze Analysissurface topographySLAMstereoscopic content productionSPECTRAL DATA RECONSTRUCTIONSPECTRAL EDGEsplicingSeam carvingSuper-resolution image transformationsmart image sensorsSQUARE APERTUREStereoscopic visionSpatiotemporal featureSCADAsemantic segmentationSpeckle Noise Reductionsimilarity analysisSmart Home SecuritySocial Media AnalyticsStructured LightSVMStegotext generationSpatial comparisonssolid state scannerSuper multi-view displayStereoscopic Visualizationsecurityslanted edgesSIGN COMPRESSIONSnowfallStereoscopic displaySpatial Light Modulatorsstereo camerasupport vector machineSilversicknessStereoscopicSpoofing detectionSMARTPHONESoftware ArchitectureSocial networkSURVEILLANCE REGIONScene analysis for intelligent robotsSTEREOSCOPIC HUMAN FACTORS AND DESIGNSHRsubjective and objective quality assessmentsensor fusionSICPScene UnderstandingSuper multiviewsatellite image enhancementSD&A award winnersSpot colorsSimplificationSurround ViewSpiking imagersSuper-ResolutionSUBBAND IMAGE CODINGStereo VisionSpatial transcriptome analysisSports analysisSerious GamestitchingSubjective and Objective video qualitySTEREOSCOPIC DISPLAYSSTATISTICAL TOOLSSERIAL-SECTION IMAGINGSpatial ActivitySlow-Motion Video Capturesecurity applicationsSearchsynchronization signalSNRSensing Technologystructure tensorSETTINGsynthetic apertureSPECTRAL SENSITIVITIESSILICON DEFECTSSD&A Video Recordings StatisticsStandardssport and athleticsSimulationSPATIAL CHROMATIC CONTRAST SENSITIVITY FUNCTIONSUPERPIXEL CLUSTERINGSaturated pixels correctionsignal averagingSymplectic numerical methodsSkincare product efficacySteerable filtersScattering MediaSingle slopesystems engineering-driven designSEMANTICsmart libraryspatial frequency responseSuper-resolutionshareable visualizationsSpikingSpatial ImagingSenser Fusionspatially varying BRDFSubjective methodologiesStatistical characterizationSnow imagingSKIN COLOR MODELSKIN DETECTIONSaliency MapSECONDARY ILLUMINATIONsmall object detectionSparse modelingStudentsSize IndependentSynthesized monochromatic basis functionsSkin cancersoftwareskin reflectancesoftware managementSpherical Harmonicssuper-resolution microscopySCENE PERCEPTIONSelf-supervised LearningSELECTIVE SEGMENTATIONSELF-EXAMPLESpectral reconstructionSHEETFED SCANNERspectral reconstructionSPATIOTEMPORALLY-ORIENTED ENERGY FEATURESscannerscene representationsparse signal recoverySMARTPHONE COLOR QUALITYStereogramSpectral ReconstructionseparationSegmentationSoftware engineeringSpatial attentionskin colourSparse CodingSignal linearitySECURITY OF EHEALTH APPSStreaming Medida for FoLD Displayssovereign document securitySynthetic DataSUPPORT VECTOR MACHINESSpatio-temporal filteringSTYLE TRANSFERspectral renderingSegmentation Refinerstereo disparitySystem performancespectral filteringsamathaSERIAL NUMBER RECOGNITIONSpatio-temporal relationsstrawberryScanpath predictionSPAD Arraysimulated light fieldSemantic DetectionSSIMSOLAR AZIMUTH AND ELEVATIONSPATIALLY VARIANT REGULARIZATIONSpatial extensionsignal enhancementSPATIALLY VARYING COLOR CORRECTIONstereopsisSTEGANOGRAPHYStereoblindnessSelf-Supervised LearningSHARPNESSSpectroscopySKIPSOFT PROOFINGSurface appearance Spatiotemporal analysisStatistical analysisSpeech-to-TextSubjective quality assessmentsubjective experimentsSkin colour measurementspeech to textSubjective testSensor ModelingSocial Shared Spacessmart home devicesStereo DisplaySYNCHRONIZATIONSpatialized ambisonic audioSPARSE REPRESENTATIONSSmartphoneSPEECH RECOGNITIONspectral tunable LED lightingSupport Vector RegressionSENSOR FUSIONStray light testingSmart Homeseed initializationSUBJECTIVE QUALITY ASSESSMENTSHADOW DETECTIONSpecular reflectionSKIN TONE REPRODUCTIONspectral colorSubjective evaluationSystem Partitioningself-interferenceSong dynastySAR imageSUBJECTIVE TESTSURFACE PROPERTIESscene analysisSocial Media IntelligenceSPATIAL FREQUENCYSENSORSSPATIAL RESOLUTIONsocial media intelligenceSCANNING ELECTRON MICROSCOPYScreeningSpatial frequency responseSUPER-PIXELSALIENCY MAPSSMILE ELEGENCE DETECTIONScientific visualizationSCIENTIFIC VISUALIZATIONSpectrometerSnowfall noise eliminationSTRUCTURAL COLORStandard Dynamic Range (SDR)SPECTRAL SIGNAL RECOVERYSEMANTICSSLIC SUPERPIXELSsecurity auditSINOGRAMspatial memorysubjective quality assessmentSecond-order isomorphismSPECULAR SEPARATIONSaliencySingle Exposuresimulationsemantic differential methodSubjective and objective visual quality assessmentspeech-to-textSensor pattern noiseself-driving carSURGERY TRAININGSurface modificationstructured lightspatial audioSynchronizedSTATISTICAL COLOR IMAGE QUALITY ANALYSISSaliency mapStereoscopic image quality assessmentShapeSpectrophotometerSobel edgesystemSiamese Networksspeech rateSide-InformedSPADSimilarity metricsSTEREO CAMERASignal Processingsport tourism and recreationsuper-resolutionSHAPE DESCRIPTORSSTANDARDIZED RESIDUALSHOT-NOISESLANTED-EDGESensing and imaging techniquesSTRESSSpace-Variant PSFSubjective StudiesSUPPORT VECTOR MACHINEScene understandingSensor FusionSTRUCTURE TENSORspectral reflectance estimationSubjective Assessment Protocolspectral samplingshakeSCENE CHANGE DETECTIONSCANNERSingle image haze removalSecret PhotographySMILE DETECTIONSURFACE INSPECTIONSocial mediaSPECTRAL REPRODUCTIONSuper resolutionsize effectSHADOW IMAGESTEREOSCOPIC DISPLAYSurface MetrologySpectrum modulatorSCENEStereo matchingSD&A Super-ContributorsSPORTS VIDEOSCINTILLATORSUBJECTIVE ASSESSMENTscene-dependencyspecies classificationSINGLE VIEW GEOMETRYSPECTRAL TRANSMITTANCESCANNED IMAGESubjective and Objective evaluationsimilarity measureSPORT ACTIVITIESSOFTWARE RAIL CAMERAskin tone classificationSCLERAsensor noisespatial attributesSPARSE REPRESENTATION OF SIGNALSSmall Face DetectorSaliency estimationSYNCHRONIZATION ANALYSISsqueeze and excitationSPATIAL BRIGHTNESSstandardizationSTEREOSCOPIC VISUALIZATIONSACCADE DETECTIONSTEREO MATCHINGsuperhydrophobicSTATE MACHINESaliency MapsSubjective and Objective Quality AssessmentSpectral similaritystripe noise removalSFRStyle TransferSpeckleSTOCHASTIC PROCESSskin segmentationSAMPLING METHODSUBJECTIVE EVALUATIONsubjective experimentSIMULTANEOUS LOCALIZATION AND MAPPINGSimulation-based trainingSiemens starSECURITY POLICYSurround View CamerasSPEED AND ACCELERATION OF CARSURVEILLANCE VIDEO OF VEHICLE CAMERASensing and Imaging Techniquesspectral sensitivitySubjective quality evaluationsecure remote desktopstructure-aware halftoningsignal detection theorystrain-resistive effectSpot coloursSEMI-PHOTON-COUNTING-LEVEL CMOS IMAGE SENSORsharpnessSIMILARITY MEASURESSCIELAB modelSeparationSecuritySegment Anything (SAM)screening echocardiogramSYMMETRY CONSTRAINTSSheet metal productionscaleSURFACE APPEARANCESpatial Frequency ResponseSemantic segmentationSPECTRAL REFLECTANCE AND TRANSMITTANCEStatistical background modelsSharpnesSemantic SegmentationSpace-VarianceSCATTERING MEDIUMSwin Transformerscreen brightnesssuper sharpnesssurrealismScreening mammographySALIENCYSpherical harmonicsSynchronizationSpatial Distance-based InterpolationSPECTRAL SUPER-RESOLUTIONSmart Image Sensorsskin colorsubjective assessmentSKIN TONESemi-supervised learningSpectral printer characterizationSpectral imagingspectral imagingSlanted Edgesurface appearanceSUBJECTIVE EXPERIMENTSSPONTANEOUS PROBLEM-SOLVING AND DECISION-MAKINGSELF-ASSESSMENTslanted edgestereoscopic, volumetric, and true 3D displaysSpatio-Temporal Supra-Threshold DistortionsScene-DependenceSMFoLD Open StandardsSHARED COLLABORATIVE REPRESENTATIONskin healthShodanSpatial frequency response (SFR)Surface MeshSPECTRALSURGICAL SIMULATIONSiamese Random Forest (SRF)Scanning camera backsignal rich artSELF-INTERFERENCE INCOHERENT DIGITAL HOLOGRAPHYSpectral Reflectance Estimationspectral reflectance spacesemi-supervised methodSKY COLOR ENHANCEMENTsurface perceptionspectralSubjective Testingsubstrate coloursSELF-PORTRAITSIMULATIONspherical harmonicsSTORY TELLINGSUPER-RESOLUTIONstereoscopic artifactsstructured light projectionsmall dataStereo ImagesSystem MTFSUBJECTIVE METHODOLOGYSingle Image Super-Resolutionsystem integrationScansecond-order statisticsSampled imaging systemSOFT TISSUESSURVEYSense of realismSemantic labeled grading scalessaliency mapSimilarity searchShannon information capacitystabilitysegmentationSTATISTICAL SIGNIFICANCESpectral fusionSurveillancespectrum-adaptive decompositionSignal rich artSteganalysisSTILL IMAGINGSearch algorithmsS3D CONTENTsmart phonesSquare Root LawSaturation enhancementSKIN COLORstereoscopic displayscan path comparisonSensor fusionSensor designsafety systemsocial media investigationSensor Evaluation MethodsStereo Camerasstereoscopic imageStructural Color PrintingSENSITIVITY ANALYSISscene change detectionSEE-THROUGHSIGNAL DETECTIONStereosparse codingsurface temperaturesuper depthseat of attentionSerendipitous InteractionSpatial resolutionSuper PDSequential analysissubjective studySELF-SUPERVISED LEARNINGSpectral BRDFSEGMENTATIONSPATIAL FREQUENCY RESPONSEspatially varying bidirectional reflectance distribution functionsSensors and ProcessorsSearch and rescue roboticspectral differenceSubjective image qualitySINGLE PHOTON AVALANCHE DIODE (SPAD)STEEP PN JUNCTION SI DIODEScene-and-Process-Dependent Noise Power Spectrumsurface preserving smoothingSMALL MULTIPLESSTEREOSCOPICSPOT COLORSspectral reflectanceSequential transfer gatesoft sensorsSMSSIFTSELF-DRIVING CARSscientific imagingSKIN GLOSS PERCEPTIONSteganographic filesystemsSCENE-DEPENDENCESelf-Supervised Learning (DINO)Signal processingself-locationsubpixel sample propertiesSurround View camerasspectral filter array cameraSPARSE CODINGSPATIAL DATABASESSignal-dependent noiseSemantic differential methodSYMMETRY CORRESPONDENCESTILLNESS DETECTIONSTEGANALYSISSUPER RESOLUTIONsampling efficiencysmartwatchSequence ModelsSPARSE RECONSTRUCTIONSurface Geometry ChangeSPECTRAL SENSITIVITYSubjective Image Qualitysecure remote serviceSUBJECTIVE VIDEO QUALITY ASSESSMENTSIGNAL PROCESSINGSTEREOSCOPIC VIDEOSCANPATHsimultaneous contrastshitsukanSATELLITE IMAGE ENHANCEMENTSatellite ImagesSUPER-INTERPOLATIONSensation of realismSOURCE CAMERA IDENTIFICATIONStereoscopic Cinema and TVSobel Edge DetectionScanning Electron MicroscopysplinesSTEREO 3D MOVIESSTRUCTURED LIGHTSYSTEM CRITERIASPATIO-SPECTRAL ANALYSISsurveillanceSaliency Detectionstereoscopic aspects of VR, MR, and XRSPECTRAL POWER DISTRIBUTIONSoftware Testingstereo visionSafetySocial Sciencessecure electionssensing and imaging techniquesspatially adaptive regularizationsteganographySunglare detectionSiamese networkSPARSITYsensor arraysynchronizationSafety applicationSensor characterizationStereo visionsparkle impressionSALIENCY MAPSpatial frequencySMALL SAMPLE SIZE (SSS)spilled coins chartSTEREOSCOPIC CINEMATOGRAPHYSpectral processingScan-pathSIPSANKEY DIAGRAMSensor ArraySIM2subject rejectionSymmetry BreakingShitsukan perceptionSUPERVISED MACHINE LEARNINGSmart GlassesSUPPORT VECTOR MACHINE (SVM)
T 
texture structureTEXTURE SEGMENTATIONTRANSMISSION MEASUREMENTTEXTURE ENHANCEMENTtone reproductionTRAP CAPACITYThermographyTEXTURE SYNTHESISTRICHROMAT MODELSTangent ImagesTEXTURE VISIBILITYTraining DatasetsTissue Sub-Region ClassificationtextileTUTHIN FILMTOP VIEWTOF CAMERATraffic Sign Recognitiontablet displayTissue FluorescenceTOMOGRAPHIC RECONSTRUCTIONTemporalTelegramTaiwanTAYLOR CONETOTAL APPEARANCEtransfer learningTexture mappingtemporal pooling methodText qualityTIME-OF-FLIGHTTraffic Signal SecurityTMO evaluationThree-dimensional/two-dimensional switchable displayTask Evoked Pupillary ResponsetranscriptionTone MappingTeachingTYPE II ERRORtoner scatteringTHREE-DIMENSIONAL (3-D) PRINTINGTile-basedTime domain continuous imaging (TDCI)TIME- FREQUENCY AUDIO ANALYSISTrackingtangibletactical training applicationsTWO TIRE ARCHITECTURETemporal DegradationTRIGGER JITTERtracking tooltransparencytraining data augmentationTEMPLATE MATCHINGTransparent layerTRANSPARENT DISPLAYtraditional tools and new toolstamper detection and localizationTOOLS AND SYSTEMStransfertranslucency perceptionthrough focusTMOtrackingTEMPORAL NOISE REDUCTION (TNR)TEXTILE HISTORYTransformTransfer learningTwo-fluxTRISTIMULUS VALUEText Fadingtraffic scenetranslucencyTEMPORAL SUPER-RESOLUTIONTDCI (Time Domain Continuous Imaging)Transmission over noisy channelsTunable diode laser absorption tomography (TDLAT)temporal noiseTime-Division MultiplexingTracking-by-detectionTHERMAL INFRAREDtransmissive samplestorch.fxTECHNOLOGYTotal mixed ration intakeText DetectionTEXTURE-BASED CODINGTEXTURE CLASSIFICATIONTEMPORAL CONSISTENCYtRANSACTwo-step cascadingtongue detectiontemperatureTRANSMITTED IMAGETEXTURE DESCRIPTORStoner fusingTIME-DOMAIN RADIO ASTRONOMYTrained ParkingTDCI (TIME DOMAIN CONTINUOUS IMAGING)tactile memoryTranslucencyTransportation SystemsTexture SynthesisTAIWANESE PHYSICALTemporal ContrastTissue slidesTEXTURE RE-RENDERINGTomatoesTargetthe probability of dangerous failureTEXTURE BLURTIME-RESOLVED IMAGE SENSORTHERMAL IMAGINGTrajectory PredictionTEXT FADINGTranslation NetworkTerrain classificationTIME-SEQUENTIAL CHARACTERISTICSTheft prevention and recoveryTraditional rear-view mirrorsTRANSFORMTOMOGRAPHYTILE VISUALIZATIONTEXT ANALYSISTransmission electron microscopythree-dimensional printingTelecentric optics systemtools and systemsTraffic Videostexture classificationtransparent layerTone-Dependent Fast Error DiffusionTopic Visualizationtime-of-flight cameratime courseTEXTURE ANALYSIStransmission mapTest chart MTFTIME-DIVISION MULTIPLEXINGTranslucenttetraphenyletheneTELECENTRIC LENStime-of-flightTexture recognitiontime of flighttransformerstone curvesTIME SEQUENTIAL OPERATIONTECHNICAL COMPARISONTEXTURETexture DescriptorsTRUNCATED SIGNED DISTANCE FUNCTIONTEXTURE REPRESENTATIONSTwo-scale depthTransfer LearningTEXTURE PERCEPTIONtotal variation (TV)Throwing BehaviorTRAFFIC LIGHT SHAPE RECOGNITIONThermal imagingTONE MAPPING OPERATORTDA3xTWO-FLUX MODELTONE MAPPINGTRANSFER LEARNINGTRAFFIC LIGHT COLOR RECOGNITIONTone mappingtexture characteristicsTask-Based Quality AssessmentTraveling wavethermal absorptionTV ContributionTwittertrue orthoimagetransitionTwo-factor authenticationTotal Variation Penaltytrench MOStextureTOMOGRAPHIC IMAGE RECONSTRUCTIONTRAININGTamura’s featureTangibleTensor displayTransformer networkTIME DOMAIN CONTINUOUS IMAGINGTime-division multiplexingTrench capacitorTime-of-flight (ToF)THERMAL GENERATION OF DARK SIGNALTubesTRANSMISSION TOMOGRAPHYtone mappingTexture retrievalTransparencyTRAFFIC CAMERATest chart qualityTRUCK CRANE OPERATIONTemporal NoiseText RecognitionTransformersTABLET TYPE DISPLAYthree wafer stacktelepresencetele-conferencetungsten trioxideTOPIC MODELINGTEXT RECOGNITIONtrench gateTextileTransformer NetworksTraining dataset constructiontemporal contrast visiontile organizationTrain data enhancementTEXTURE LOSSThe Candlelight MasterTIKTexture detail preservationTemporal Contrast Sensitivity FunctiontcadTUBULE SEGMENTATIONtransmission losstemperature sensorTranscodingTexture lossTRAFFIC LIGHTteleoperationtext qualityTransparent displayTransparentthermal sensitiveTwo-view light fieldtraining simulationTradeoff ParametersTransmittance measurementtotal variationThitsiolTWO-DIMENSIONAL CODINGtime seriesTeleoperationTransparence & absorbanceTRAFFIC LIGHT RECOGNITIONTRANSPARENT PLASTICTAXONOMYTEACHING TOOLTaguchi methodTHREE.JSTask PerformancetechnologytractographyTetracell image sensorTensor-Product B-Splinetwo-level envelopeTime-of-flighttime studietrainingTopology and GeometryTools and systemsTHERMAL IMAGERYTRANSFORM DOMAINtele angle optical systemtwo dimensional colour appearance scalesTCADtextilesTASK-BASED PARAMETRIC IMAGE METRICTRANSMISSION NOISETraffic AccidentTotal appearanceTRANSMISSIONTRAP LEAKAGE RATETopographytheoretical upper boundtime-series datathermal imageTELEMEDICINEtest artifactsTRANSLUCENCYTrilateral kernelTEXTURE FEATURETexture featuresTire Defect DetectionTime division multiplexingTESSERACTTRANSLUCENT MATERIALTwo-Channel EncodingTONER LEAKAGETextureTRAFFIC DATATemporal SensitivityTemporal change detectionTONGUETrainingTRISTIULUS VALUESTone Curve Compensationtraining moduleTHREE-DIMENSIONAL (3-D) PRINTERTranslationThree-dimensional DisplaysTiO2TONER USAGE ESTIMATIONTemporal SamplingTOP WINDOW RECOGNITIONTools and SystemstrichromatTime-to-First-SpikeTask interdependenciesTYPE I ERRORtolerance ellipsoid
U 
Unsupervised clusteringUNDERWATER PHOTOGRAPHYUser Performanceultrasound imaging phantomUnmixingUser studyuniformity measureUser interfaceUnsupervised learningUnder Display CameraupdateUnscented Kalman FilterUAV DETECTIONUnassigned distance geometry problemUnderwaterUNSHARP MASKINGUser FacilityUSER STUDYUNIFORMITYULTRA HIGH DEFINITIONUNMANNED AERIAL VEHICLESuniform colou spaceUdder classificationULTRA SHORT THROW PROJECTORunique huesUnityUnit sphereUnlabeled dataUNEQUAL RESOLUTIONUSER-ADAPTATIONUniform color spaceultrawide angle of viewULTRA-HIGH SENSITIVITY CAMERAurban trafficUnreal Engine 5User interaction with heterogeneous datauseful field of viewUser feedbackULTRAHIGH DEFINITION (UHDTV)UTILITYUnderwater image enhancementUV-F.Under-exposedusabilityUncertaintyUSER INTERFACEUnequally-Spaced Fast Fourier TransformUsage ScenariosUnderwater image formation modeluniformityuser visual fatigue assessment modelUrushiolUV INKJETUnsupervisedultrasound elasticity reconstructionUSE CASESUniform Color SpacesUltra-high-speeduhdUV WASTERMARKuser interactionuser studyUltra-fast lensUnique hueUltraviolets (UV)User ExperienceUV-curingUNSUPERVISED VIDEO SEGMENTATIONunderwater sounduser experienceUHD SIGNAL MEASUREMENT TOOLU-netUAVSUTLIZATIONUnder Panel CameraUSDZUser identificationUAVUser characterizationUltraviolet-Induced Visible FluorescenceUFOVULTRAHIGH-DEFINITION TELEVISIONuser friendlyULTRA HIGH SPEED IMAGINGUNCERTAINTYUser perceptionUser Interfaceunderground mappingULTRASONIC MODELINGUNSUPERVISED MACHINE LEARNINGuncertaintyultrafine particleU-NetultravioletUNDERWATER IMAGE ENHANCEMENTuniform color spaceUser Generated Video Contentunmanned ground vehicleUNSUPERVISED LEARNINGUser Generated Content (UGC)Unreal EngineUser PreferenceUHD SIGNALS
V 
Visual analyticsVulnerability Managementvision assessmentvehicle controlVISUAL DEFICIENCYVR and True 3D DisplaysVIDEO FORMATSviewvisual acuityView reprojectionVISUAL INSPECTIONVISUAL CLARITYVolumetric Videovisual cognitionvideo processingVideo SurveillanceVR distance perceptionVirtual Reality VIDEO RESOLUTIONvirtual reality UI and UXVirtual adversarial trainingVISUAL ANYLITICSVISUALIZATIONvideo analysisVELOCITY DIFFERENCE PERCEPTIONVideo analysisvirtual point light sourceVolume RenderingVRI GAMING MODULEVISUALLY LOSSLESSvideo perceptionVincent van Goghvirtual displayVIDEO ANALYTICSVideo processingvideo editionVRVIEWING EXPERIENCEVIDEO FORENSICSVISUAL AWARENESSVisual PerceptionVirtual,visual modelVehicle re-identificationVIRTUAL REALITY INSTRUCTIONAL MODULES (VRI)Visual perceptionvr designVulnerability Remediationview recommendationVIDEO PROCESSINGVision TransformersVideo analytics systemsVergence-accommodation mismatchVisual fatiguevisual perceptionVOLUMETRIC TERRAINVOCVISUAL EXPERIENCEvisual comfortVFX Environmentvisual semioticvisual-selection methodVirtual and Augmented Reality in Education, Learning, Gaming, ArtVintageVMAF metricVIDEO ANALYSISVIDEO QUALITYvisual experimentVoltage domainVARIABLE-INTENSITY TEMPLATEVideo CodingVIDEO CONTRAST ENHANCEMENTVIEWSVideo forensicsvideo quality assessmentVISUAL PERCEPTIONVIRTUAL REALITY UI AND UXVISUAL DISCOMFORTvisual transfer functionVehicle DetectionV1VIEWING BEHAVIORVIDEO STEREOVISUAL DATASETVirtual and Augmented RealityVisual saliencyVisualization ToolsVideo Portrait Segmentationvisual qualityVariable precisionVulnerable Road Users (VRU)VISUALIZATION TECHNIQUESvision, audition, haptics, multisensoryvisual difference predictorvideo codecsView synthesisVECTOR FIELD VISUALIZATIONvisual perception modelVisual AnalyticsVisual documents trackingVolumetric compressionView SynthesisVisual adaptationvideo analyticsVirtual scenesvisual cortexVISUAL ATTRIBUTESVISUAL QUALITY ENHANCEMENTvolume renderingVisual fidelity in virtual realityViewing behaviorVisual SLAMVIRTUAL MATERIAL APPEARANCEVisual place recognitionVOLUME RENDERINGVideo Assistant Referee (VAR)video segmentationVOLTAGE MODEVIRTUAL AND AUGMENTED REALITY IN EDUCATION, LEARNING, GAMING, ARTVISIONVALIDATIONVisual localizationvisual computingvipasyanaViewing conditionVisual Quality Across Displays and Viewing Conditionsvisual judgmentVolumetric video compressionVEHICLE RE-IDENTIFICATION (VRI)Visual Quality AssessmentVFXVISUAL PLACE RECOGNITIONVIDEO QUALITY ASSESSMENTvideo quality analysisVisual appearanceVirtual EnvironmentVTK-mVULNERABILITY TESTINGVVCVIEWER PREFERENCEVIDEO CODECSVIRTUAL REALITY (VR)Video Frame InterpolationVISUAL ANALYTICSvisual fatigueVR/360° videosvisual appearancevideo codingVisual appreciationVISUAL EXPERIMENTvignettingVISUAL CORTEXvirtual and augmented reality (VR/AR)Visual Assessmentvisually lossless compressionVIDEO SUMMARIZATIONvisible watermarkvisibility of gradientsVOXELvideoVRI moduleVEHICLE POSE ESTIMATIONVirtual EnvironmentsVision, audition, haptics, multisensoryVIRTUAL TRACKING SHOTVisionvolume analysisVisual noiseVisual InspectionVIDEO QUALITY EVALUATIONVIRTUAL REALITYVideo quality evaluationVision TransformerVISUAL FIELD DEFECTVideo qualityVISUAL PERCEPTION FIELDVIDEO CODINGVQAvirtual reconstructionVisual-HapticVisual and Data Analyticsvisual texturesVR and ARvisual experimentsvisibility imagesVIDEO COMPOSITINGVideo Deepfake Detectionviewing distanceVideo quality assessmentVisualization and ExplorationVirtual Studiovisualizationvisual cuesvisual glarevisual analyticsvirtual and augmented reality systemsVECTOR HALFTONINGVirtual/Augmented Reality ExhibitionsVIDEOCONFERENCEVirtual Realityvisual literacyVirtual crowdsVISUALLY IMPAIREDVR180 videosVCXVisual similarityVIEWER EXPERIENCEVERNIER ACUITYVirtual viewVideo source verificationVideo post-processingVISUALLY INDUCED MOTION SICKNESSVISUAL EFFECTS PIPELINEvisual artvisual featuresVideo Object TrackingVISUAL ARTVoice authenticationVectorVIDEO QUALIYvehicle driver imagingVISUAL FATIGUEvideo hashVISUAL INFORMATION ANALYSISvisual evaluationVIDEO SURVEILLANCEViewing conditionsVISUAL COMFORTVideo degradationsVergence-accommodation conflictvisual patternsVirtual Simulation PlatformsVR ArenaVISUAL INFORMATION PROCESSINGvergence accommodation mismatchVessel orientation recognitionVisual ComfortVirtual realityVR, AND TRUE 3D DISPLAYSvideo thumbnailVISUAL QUALITYVISION, AUDITION, HAPTICS, MULTISENSORYVideo TrackingVulnerability Scanningvideo summarizationVideo QualityVideo motionVinylcarbonatesvergenceVideokymographyvividnessVision transformerVisual Designvisual and data analyticsVISUAL ATTENTIONVisual systemValue certaintyVisibilityvisual attentionVESTIBULARVARIANCE OF LAPLACIANVISIBLE AND THERMAL INFRAREDVideo compressionViewing DistanceVIDEO COMPRESSIONvisual noiseVR and AR in education, learning, gaming, artvariational autoencoderVehicle EnvironmentVirtual and Augmented Reality SystemsVideo GamesVirtual Reality (VR) and Augmented Reality (AR)Video Super-ResolutionVehicle Type RecognitionVP9virtual productionVISION STANDARDSVisual Representation LearningVISION RESEARCHValidationVersatile Video CodingVISUAL ODOMETRYVISUAL MODELVIEWING ANGLEVisual human factors of traditional and head-mounted displaysVocal Foldvideo quality metricVNIR-SWIRVORA-VALUEvisual transformerVisual AnalysisVIQETvision transformervision and artView normalizationvisual and cognitive issues in imaging and analysisVideo ProcessingVisual Object Trackingvirtual realityvideo surveillanceVisibility EnhancementVideo conferenceVIDEOVisualizationVisualisationVISUAL REPRESENTATIONVirtual Reality UI and UXVR gogglevector visualizationVKGVIDEO OBJECT SEGMENTATIONVisual and cognitive issues in imaging and analysisVIDEO CODECVision visualizationVisual Comparisonvisualization recordingsVIRTUAL AND AUGMENTED REALITY SYSTEMSVISUAL SYSTEMVISUAL AND COGNITIVE ISSUES IN IMAGING AND ANALYSISVR imagingVIDEO STITCHINGVideo codingVIEWING DISTANCEvideo qualityVehicle detectionVirtual imagevisualization literacyvideo bitrate controlVisibility AppearanceVIDEO AERODYNAMIC ANALYSISvariance analyisisVideo contentVISIBLEVIEW SYNTHESISVISUAL APPEARANCEVirtual Reality , Hybrid Reality, Mixed Reality, Stereoscopic 3D, OLED, Augmented Reality, Stereoscopic CrosstalkVQEGVehicle-Pedestrian interactionVIEWING DIRECTION CONTROL CAMERAVisual Searchvisionvideo representationVISUAL DETECTIONVIDEO COMMUNICATIONVision-based worker assistancevertical gatevisual human factors of traditional and head-mounted displaysVULNERABILITY SCANVideo Quality Assessmentvinegar syndromeVideoViterbi algorithmVehicle E/E ArchitectureVisual Attentionviewport predictionVIRTUAL ENVIRONMENTVEILING GLAREvibrationVISIBILITYView InterpolationVIDEO IN PRINTED PRODUCTViewing angleVR trainingVideo Feature ExtractionVP10VIEWPOINTvalue-added applicationvirtual depth
W 
WCGWEAVINGWELDINGWhite channelWearableWIDE DYNAMIC RANGE (WDR)Whiteboard image enhancementWebsite SecurityWHITE POINTWEB SERVICESwith reference experimentwaste2energyworkflowswoodWIDE COLOR GAMUTWoodburytypeWearable Electronics and EOGWeb-basedWOODBURYTYPEWRITER IDENTIFICATIONWEARABLE HAPTICSWide color gamutWaveguide StructureWIKIPEDIA BOOKSwildlife surveyWarpingWeb-based visualization systemWide field of viewWave-front processingWHITE INKWEBCAMWhiteboard image qualityWEB SCRAPINGwatermarkingWHITEBOARD IMAGE ENHANCEMENTWAVELETSWheat SpikesWork InstructionsWEB-BASED VISUALIZATIONSWordcloudsWavelength division multiplexingWeb of Thingsweb platformWriter Identificationweb conferencing servicesWalking simulatorWCG (wide color gamut)wraparound GaussianwhitenessWHITE BALANCEWHITE BALANCINGWLAN LOCALIZATIONWITHOUT MECHANICAL MOTIONWEBMWide ActivationWAVEFRONT CORRECTIONWiener InverseWindshield displayWET -COLLODION PROCESSWHITE-BALANCEWatermark CNN weightsWORKFLOWSwavelet transfer networkwayback-machinewhite Gaussian noiseWATERMARKINGwatercolorWIENER ESTIMATIONWRAPPER APPROACHWeb applicationWaveletsWien's approximationWATER VESSELSwriter verificationWorking DistanceWEBGLWATER BASED INKWATER REGION DETECTIONweb imagingweatherWEIBULL DISTRIBUTIONwhitening and coloring transformsWAVELETWEB APPLICATIONWEB INTERFACEWhitenweb-designWide viewing zoneWide Color Gamut (WCG)Whole-Slide ImagingWorkflow automationWatermarkingwarp/blend meshesWearablesWavelet transformwide color gamutWhiteboard content readabilityWebWEBwhite appearanceWorkplaceWatermarkWDRweighted nuclear normWAVE ABERRATIONWHITEBOARD EXTRACTIONWebPWATERLIGHTWide Color Gamutwasre sortingWHITEPOINT ADAPTATIONWavelet on graphswhole-slide imaging in digital pathologyWAVELENGTH SELECTIONWavelength dependencyWide color volumewide colour gamut (WCG)Whiteboard CodingworkflowWiFi Capturingweb
X 
X-RAY IMAGEX-ray phase contrast tomography (XPCT)X-ray Ptychographyx-ray phase contrast dark field tomographyX-ray CTX-ray CT Image ReconstructionX-RAY CT IMAGE RECONSTRUCTIONX-Y TABLEXRF IMAGINGXR
Y 
YOLOv8YOLOv5YOLOYolov5You only look once v3 (YOLOv3)You only look once (YOLO)YOLO-RYouTubeyolo
Z 
Z numberZERNIKE MOMENTSZERNIKEZero Parallax SettingZoom FatigueZEISSZ-type SchlierenZernike polynomialZebra Embryo
0 
0.8um pixel
1 
1-bit matrix completion180 degree images100 Hue test1/f noise133-MEGAPIXEL108 Megapixel1st and 2nd FM generation 3D halftoning1 MICRON PIXELS
2 
2D AND 3D CONVERTIBLE DISPLAY2D/3D imaging, high performance computing, imaging systems, efficient computations and storage2.5D PRINTING2.5 D printing2D printing2AFC2D2D-TO-3D CONVERSION ARTIFACTS2-D barcodes2D to Hologram conversion2D DCT2.5D2.5D reconstruction2D and 3D video2D VIEWS2D-plus-depth video2-d scale2D metrics2.5D printing
3 
3D recursive search3-T pixel3D halftoning3D Range Data Encoding3D Computer Graphics3D Models3D Meshes360-deg quality assessment3D and 2D3D STIMULI3D SHAPE INDEXING AND RETRIEVAL3D shape analysis3D MODELLING3D/4D SCANNING3D point cloud3D-shooting3-D RECONSTRUCTION360 degrees video360-degree3D mesh3D-color perception3D communications3D object shape3D EDUCATIONAL MATERIAL360° STEREO PANORAMAS3D Compression and Encryption3D Iterative Halftoning3D reconstruction3D image compression3D MESH360-degree video streaming3D Lidar3D Video Communications3D PROFILE3D/4D DATA PROCESSING AND FILTERING3D Shape Indexing and Retrieval3d localization3D Video3D TV3D depth-map3DMM3D MESHES3D DISPLAY3D cinema and TV3D-human body detection3D SCENE RECONSTRUCTION AND MODELING3d3A ALGORITHMS3D mesh simplification3D IMAGE3D range scanning360-DEGREE IMAGE3D rigid transformations3D vision3D3D Reconstruction3D USER INTERFACES3D COMPRESSION AND ENCRYPTION3D glasses3D localization3D-printing3D displays3D Quality360-degree imaging3D RECONSTRUCTION3D compression3D VISUALIZATION3D-Anisotropic smoothing3D surface structure based halftoning3D STACK3DCNN3D Display3D audio360 Video3D INTERACTION3D ACQUISITION ARCHITECTURE360° VIDEO3D imaging3D localization and mapping3D digitization and dissemination3D RECOVERY3D Print Appearance3D-assisted features3D range geometry3D colour Digital Image Correlation3D Printing360 degree images3-D SHAPE RECOVERY3D Mapping3d mapping3D printing3D SALIENCY3D Communications3D printer360x3D scene capture3D print3D Scene Reconstruction and Modeling3D visual representation3D-high efficiency video coding3D recovery3D shape3D scene classification3D encoding3D Point Cloud3D Color Printing3d video3D HALFTONING360° video3D warping3ARRI footage3D modeling3D Imaging3D DIGITIZATION METHOD FOR OIL PAINTINGS3D TRANSFORMATION360-degree Image35MM FILM DIGITIZATION3D Modeling3D Digital Image Correlation3D projector3D position measurement of people3D human-centered technologies3D refinement3D model3D-CNN3D Halftoning3D camera3D Scene Reconstruction3D Data Sources3D Range Data3D connected tube model3D affine transformation3D Tracking3D adaptive halftoning3D scene flow estimation3D Vision3D PRINTER360-degree videos3D capture3D scanning3D modelling3D Image Processing3D/4D Data Processing and Filtering360VR3D optical scans360 IMAGING3D Saliency3D Compression3D Curvelet3D RANGE IMAGING3D surface3D digital halftoning360-degree video3D Immersion3D objects3D/4D Scanning3D shape indexing and retrieval3D theater program listing3D data processing3D surface reproduction3D video processing3D video360-degree content3D display3D MODEL3D Measurement3D CAMERAS360-degree art exhibition360 panorama3D Telepresence3D-LUT3D Morphable Model3D stereo vision3D Data Processing360-degree images360-degree image projection3D PRINTING3D Object Detection3D Range Data Compression360-video
4 
4D scanning4D PRINTING4K4T PIXEL4D-printing4K resolution
6 
60 GHz Wireless6-DOF6DoF
7 
7-1 MICRON PIXELS
8 
8K UHDTV8K SUPER HI-VISION (SHV)8K8K STEREO IMAGING
 
image matching Subjective experiment Support Vector Classification (SVC) Image Orientation capture and post processing workflow Multi lane detection Facsimile Remosaicing image enhancement image quality assessment Computer Vision IMU extrapolation AI ISO 12233 silicon-on-insulator (SOI) Structural artifact Mining Documentation Open source Hair Rendering Autonomous vehicle Denoising convolutional neural network System Simulation Changed Based Segmentation Mixed Reality effectiveness of training Realistic mannequins Automobile medical Psycho-Physiological Measurement Classification Multi-scale Autoencoder Network Neural Network Visual resolution Visualization. Art Analysis Event modeling UAV Automated vision testing multimedia security Multispectral Biometrics Optical Model 3D interaction techniques Remote operation image embedding machine learning mean opinion score (MOS) prediction of despeckling efficiency History non-expert Augmented reality Machine learning Authentically-Distorted Database redundant discrete wavelet transform (RDWT) hedonics Microscopy MRI Ligament Analysis spectral database depth encoding Crossed mirror arrays Archaeology Preservation computational imaging prism TDA Processor computer vision Compression performance Mapping film restoration Naked-eye 3D display Embedded Systems Pattern artifact all pixel AF Non-RGB Lidar False color embodiment Cattle traits color filter array (CFA) svBRDF Environment Simulation thermal image variable precision Meanings OCR synthetic data Field-of-View 360° videos U-Net Camera s-SFR Depth sensing Artifact RGB-D camera Multitask Learning Point cloud Modulation transfer function Thermal Image object classification Convolutional Neural Network Virtual reality (VR) Color Blind Machine-to-Machine transmission Event simulation optical simulation video frame interpolation Temporal chromatic adaptation Multi-Gene genetic programming Adversarial attacks image processing archives Explainable Artificial Intelligence de-mosaic optical phased array smartphone app Computer vision Machine Learning Augmented Reality Image quality metrics high dynamic range imaging Pruned ResNet camera calibration Visual noise Point clouds Drawing image perturbations Image Edges Image Segmentation MEMS specular detection segmentation Sentinel-1 Signal Falloff image super-resolution systematic review Algorithms Disocclusion Accountability Video Artifacts Digital Pixel Sensor Sensor Fusion FPN compensation Poisson-Gaussian Noise object recognition FIAF Eye Trackers workflow management moving-object detection Light spectrum analysis Pose estimation Forchheim Image Database White point binary segmentation texture perception weighted integral 3D camera Epipolar Image Plane Vulkan Conditional Random Fields judiciary image quality Automotive Procedural Rhetoric Certification color model Duplicating positive immersive VR Image Re-Identification Neural Networks deep learning Nursing Education illuminant Image Quality Metal artifact reduction optimization inverse problems automated labeling Interactive convolutional neural network Artificial Intelligence circle detection glossiness measurement system signal processing Deep Learning Neuromorphic Imaging IoU Multispectral RTI Cybersickness Discomfort Information processing RGBIR Sensor color distribution Dolby Vision pixel error model Artificial intelligence time of flight Gray-Level Co-Occurrence Matrix (GLCM) localization method DRA camera response function explainability Correlation Predictor Rendering Acne Video Quality LED illumination Column-parallel ADC Neural networks Surgery Visualization Image Processing retro-reflector diffraction. Multi-label EfficientDet. Hair dye Deformation assessment Stereoscopic display Mean Opinion Score halftoning semantics Principal Component Analysis RTI color correction Interactive Narrative Color space Data collection Object Detector studio photography Latency AV Open Source Image alignment BRDF Integrity verification color difference emotions statistical analysis Image processing Smart City. TCG Schizophrenia Neural net accelerators Spectrally extended imaging discharge of justice domain adaptation Max-Margin object detection (MMOD) building evacuation exposure bracketing multiple conversion gain transfer learning game model visualization correlation analysis slanted edge Archival theory Driving Automation Deep learning Subjective visual experiment Discolorization KG Locally Weighted Regression Art Image Forensics SfM layout mobile phone Visual Design infrared imagery A/D converters Convolutional Neural Networks material appearance visible image AV1 auditing canola seeds Quantifying Quality acrylic paint Digitization Fourier ring correlation Image classification SLAM image classification Chatbot Subjective quality evaluation haptic perception image visual quality assessment Pigmentation Evaluation Haar cascade classifier eye tracking scanning back ResNet HDR laboratory setup Material Capture UX Design white balance Quantization Single value decomposition Hand gesture cinematography crossmodal associations Geometry Comparison see-through SME phase-shifting Performance evaluation Variance-stabilizing Transformation Multimodal Sensor Fusion situational awareness Storytelling Vision processors Visual Attention skin color image denoising Camera Noise 3D displays Mental Commands Face recognition image deblurring impulse noise removal Organic video Natural language understanding Demosaicing Writing Access despeckling Noise reduction Reconstruction Layers Convolutional neural network cosmetic recommendation imbalanced data Visualization Robust photography Method of adjustment Natural Language Processing Spatial frequency response Trustworthiness single-slope ADC Shack-Hartmann Wavefront Sensor Scanner dataset generation Forensic Data Model geometric distortion VIS-NIR Imaging Skilled Subject colors Saliency prediction Spatial Frequency Response (SFR) Volumetric Reconstruction Paper Fixatives super-resolution Medical Application image analysis. Symbolic Regression low power DXOMARK Image quality evaluation camouflage virtual reality image stacking Data Augmentation modulation transfer function (MTF) artificial intelligence style transfer Open Access New perspective views. Vanitas MTF CNN Montage Detection virtual target Timecourse Color distortion 3D sensor SPD of illumination information behaviors Offset calibration Dual-energy CT enhancement Pyramid 3D content detection unpaired software Socrates Icon noise model odors GIS ATR video reconstruction Sketching 3D integration Interaction Design Image Restoration multicolor LED Performance assessment Image processing image distortion Painting data visualization. Photon Transfer Curve depth compression Optical Coherence Tomography (OCT) Cultural heritage texture synthesis MLICs maniscripts temporal dependency model Dentistry Fisheye images forgery Calibration image analysis color cube Wrinkle H.264 bitstream ghost Loss Function Interferometry Workflow Image color adjustment color appearance panorama NLP Camera ISP barely open books perception dichromatic reflection model Drones Hair AR service ancient Hebrew dataset Webcam Interdisciplinary aspects User Study Video Conferencing Near Infrared Imaging Signal-to-Noise Ratio Multicamera remote sensing image quantum efficiency Multiobjective Optimization Navigation least squares fit Quality Assurance RGB-D image Multi layer perceptron expert camera pose head-mounted display Traffic light differentiation Adversarial Network low noise Paradata SNR10 Stereoscopic. Autonomous Driving Magic Leap One Human Factors and Ergonomics face recognition Visual attention DCRA DeepFake Detection camera calilbration Novice Subject Spectral Analysis Original negative Camera identification Augmented Telepresence Recurrent Neural Network IEEE P2020 Smartphone image quality evaluation bonding Reinforcement Learning R&D Partnership Portal Yellow/Blue forced-choice experiment Frameworks Object Detection SFR Semantic Knowledge Graph Full Reference Method Local binary pattern histogram (LSBH) noise evaluation Quality of Experience (QoE) Deep learning. light-field Alignment Infrared Image Generation Dresden Image Database open-source software compression Quality control In-Cabin Monitoring Computer vision task caustics ADAS Color tolerance olfactory integration co-presence neural network Unity game engine Focal Stack image demosaicing Self-supervised learning scatterplot Virtual Reality strategic improvements Direct Sparse Odometry Data Visualization Ground truth T1-weighted Phase reconstruction multiclass e-SFR silicon photonics Collaboration image clarity enhancement Noise Multispectral imaging multispectral Illumination Awareness Network HDR10 U-net ISO12233 small and medium-sized enterprises Domain Adaption ESP32-CAM Digital restorer image inpainting Faster RCNN Genetic gain. H.265/HEVC Virtual Reality Transfer Learning Vision testing Hololens Heat Map Gaming Coco format Vison Mathematical visualization Image Database psychophysics specular and translucent materials Style Transfer convolutional neural networks
[ 
[Bmin]Cl ionic liquids
 
 Filters
Month and year
 
Keywords filter
spatial  
Regular Article
  80  26
Image
A Study of Spatial Chromatic Contrast Sensitivity based on Different Colour Background
  • spatial
  • contrast sensitivity function
  • different colour background
Qiang Xu, Qichen Ye, Rafal Mantiuk, Ming Ronnier Luo
Pages 236 - 240, November  2022,  ©2022 Society for Imaging Science and Technology 2022
  DOI
10.2352/CIC.2022.30.1.41
Volume 30
Issue 1
View  
Abstract

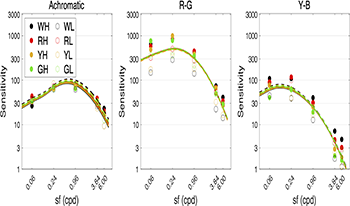
The goals of this work are to accumulate the experimental data on contrast sensitivity functions and to establish a visual model that incorporates spatial frequency dependence. In addition, the experimental results from fixed-size and fixed-cycles stimuli and from different luminance levels were compared. Such a model is highly desired for applications that rely on image quality and to serve the lighting and imaging industries. The detection thresholds have been measured for chromatic contrast patterns at different spatial frequencies. The experimental parameters included: (1) four colour centres (white, green, yellow, and red), which were recommended by the International Commission on Illumination (CIE), at two different luminance levels for each colour centre; (2) three colour directions for each colour centre, namely luminance, red-green and yellow-blue; (3) five spatial frequencies, 0.06, 0.24, 0.96, 3.84, and 6.00 cycles per degree (cpd) for fixed-cycles stimulation, in which two spatial frequencies, 0.24 and 6.00 cpd, were also chosen for fixed-size stimuli. In this experiment, a 10-bit display characterized by GOG model was used to obtain contrast thresholds of different colour centres by 2-alternative forced choice method and stair-case method. The experimental results revealed different parameter effects (colour centres, luminance, colour direction, fixed cycle/size), and also supported McCann's conclusion that the number of cycles affects the comparative sensitivity. Most importantly, a cone contrast model was successfully developed by fitting the visual test data (fixed number of cycles). The model could accurately predict the contrast sensitivity of different color centers, spatial frequencies and stimulus.

Digital Library: CIC
Published Online: November  2022
Articles
  30  6
Image
Cartography as Spatial Representation: A new assessment of the competing advantages and drawbacks across fields of science
  • cartography
  • spatial
  • representation
  • mapping
  • distortion
  • history
Christopher W. Tyler
Pages 156-1 - 156-10, January  2021,  © Society for Imaging Science and Technology 2021
  DOI
10.2352/ISSN.2470-1173.2021.11.HVEI-156
Volume 33
Issue 11
View  

The history of cartography has been marked by the endless search for the perfect form for the representation of the information on a spherical surface manifold into the flat planar format of the printed page or computer screen. Dozens of cartographic formats have been proposed over the centuries from ancient Greek times to the present. This is an issue not just for the mapping of the globe, but in all fields of science where spherical entities are found. The perceptual and representational advantages and drawbacks of many of these formats are considered, particularly in the tension between a unified representation, which is always distorted in some dimension, and a minimally distorted representation, which can only be obtained by segmentation into sectorial patches. The use of these same formats for the mapping of spherical manifolds are evaluated, from quantum physics through the mapping of the brain to the large-scale representation of the cosmos.

Digital Library: EI
Published Online: January  2021

Keywords

[object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object] [object Object]